



March 14, 2025
Here is a fun Pi Day puzzle for all of the math enthusiasts out there, courtesy of Fiddler on the Proof:
You are planning a picnic on the remote tropical island of 𝜋-land. The island’s shape is a perfect semi-disk with two beaches, as illustrated below: Semicircular Beach (along the northern semicircular edge of the disk) and Diametric Beach (along the southern diameter of the disk).
If you pick a random spot on 𝜋-land for your picnic, what is the probability that it will be closer to Diametric Beach than to Semicircular Beach? (Unlike the illustrative diagram above, assume the beaches have zero width.)
Extra Credit: Suppose the island of 𝜋-land, as described above, has a radius of 1 mile. That is, Diametric Beach has a length of 2 miles. Again, you are picking a random point on the island for a picnic. On average, what will be the expected shortest distance to shore?
Alright, give it some thought. When you are ready, see the answer below!
******************************
SPOILER ALERT!
******************************
Solution:
This is one of the puzzles that I call "The Avengers of Math Puzzles", because it involves the use of different math disciplines coming together elegantly in order to solve the problem. Here, our heroes are: geometry, probability, and calculus.
First, using a little bit of geometry, we see that there is a line of symmetry running down vertically in the middle of the semicircular pi island. This means that we can just focus on one half of the island, say the right one, for our analysis and essentially cut our work down in half. Then, employing analytic geometry, we are going to map the island onto a coordinate system. We first let the center of the would-be circle be the origin on a Cartesian plane. Then, without loss of generality (WLOG), we let the semicircle have a radius of 1. This means that the semicircular beach of the pi island has the following equation:
\begin{align} x^2 + y^2 &= 1, \quad y \ge 0 \\ \end{align}
As stated in our symmetry analysis, we are going to focus on the right half of the island. This means, we can let \(x \ge 0\) as well.
Using probability, the answer to the original puzzle is simply the ratio of the area of the region where all points are closer to the diametric beach than the semicircular beach to the area of the entire island, which is just \(\pi/2\). In order to find the area of the former, we need to seek out the boundary curve separating the two regions. In other words, all points on that boundary curve will be equi-distant to both beaches. This boundary curve will be symmetric about the y-axis. Let's find the equation of this curve.
Still focusing on the right half of the island, let us assume a point within it, say \((a, b)\), such that \(a \ge 0\), \(b \ge 0\), and \(a^2 + b^2 \le 1\). The distance between this point and the diametric beach is simply \(b\). For the distance between this point and the semicircular beach, we define the distance as the length of the line segment between this point and the point on the semicircular beach such that the line segment is perpendicular to the tangent line passing through the point on the semicircular beach. This is where calculus comes in, and there will be lots of it.
Let a point on the semicircular beach be \((x_0, y_0)\). The slope of the tangent line passing through that point will be derived via derivative calculus, as follows:
\begin{align} x_0^2 + y_0^2 &= 1\\ \\ 2x_0 + 2y_0 y_0' &= 0 \\ \\ y_0' &= - \frac{x_0}{y_0} \\ \end{align}
So the slope of the tangent line is \(- \frac{x_0}{y_0}\). Therefore, the slope of the line segment connecting \((a, b)\) and \((x_0, y_0)\) is \(\frac{y_0}{x_0}\), since two lines are perpendicular to each other if the product of their slopes is -1. However, slope is also rise/run. This means:
\begin{align} \frac{y_0 - b}{x_0 - a} &= \frac{y_0}{x_0} \\ \end{align}
The above equation is quite peculiar, and the trivial solution for \((a, b)\) is \((0, 0)\). This makes sense as that is the definition of the center of a circle, as the center point is equi-distant to all points on the circle. Moving away from this trivial solution, we can explore further:
\begin{align} \frac{y_0 - b}{x_0 - a} &= \frac{y_0}{x_0} \\ \\ x_0 y_0 - b x_0 &= x_0 y_0 - a y_0 \\ \\ a y_0 &= b x_0 \\ \\ \frac{y_0}{x_0} &= \frac{b}{a} \\ \end{align}
Since both \(a\) and \(b\) are non-negative, we can square both sides of the equation without impunity. Using the fact that \(x_0^2 + y_0^2 = 1\), we continue:
\begin{align} \frac{y_0}{x_0} &= \frac{b}{a} \\ \\ \left(\frac{y_0}{x_0}\right)^2 &= \left(\frac{b}{a}\right)^2 \\ \\ \frac{1 - x_0^2}{x_0^2} &= \frac{b^2}{a^2} \\ \\ a^2 - a^2 x_0^2 &= b^2 x_0^2 \\ \\ x_0^2 &= \frac{a^2}{a^2 + b^2} \\ \\ y_0^2 &= \frac{b^2}{a^2 + b^2} \\ \\ x_0 &= \boxed{\frac{a}{\sqrt{a^2 + b^2}}} \\ \\ y_0 &= \boxed{\frac{b}{\sqrt{a^2 + b^2}}} \\ \end{align}
So, we just figured out the relationship between \((a, b)\) and \((x_0, y_0)\). We can use this when calculating the distance between \((a, b)\) and \((x_0, y_0)\). Using the Euclidean distance formula, we have:
\begin{align} \text{distance}^2 &= (x_0 - a)^2 + (y_0 - b)^2 \\ \\ &= x_0^2 - 2a x_0 + a^2 + y_0^2 - 2b y_0 + b^2 \\ \\ &= (x_0^2 + y_0^2) - 2(ax_0 + by_0) + (a^2 + b^2) \\ \\ &= 1 - 2\left(\frac{a^2}{\sqrt{a^2 + b^2}} + \frac{b^2}{\sqrt{a^2 + b^2}}\right) + (a^2 + b^2) \\ \\ &= 1 - 2\left(\frac{a^2 + b^2}{\sqrt{a^2 + b^2}}\right) + (a^2 + b^2) \\ \\ &= 1 - 2\sqrt{a^2 + b^2} + (a^2 + b^2) \\ \\ &= \left(1 - \sqrt{a^2 + b^2}\right)^2 \\ \\ \text{distance} &= \boxed{1 - \sqrt{a^2 + b^2}} \\ \end{align}
Another way to interpret the above result is to realize that the distance between any point and the arc boundary of the semi-circle (or the edge of a circle) is simply the radius of that semi-circle (or circle) minus the distance between that point and the center. This result holds because, well, any point inside a semi-circle or a circle lies on a radius.
This means that the shortest distance to any boundary for a point \((a, b)\) inside the island is:
\begin{align} \text{distance} &= \min{\left(b, \; 1 - \sqrt{a^2 + b^2}\right)} \\ \end{align}
Now, we just need to equate the two distances to find the boundary curve, as follows:
\begin{align} 1 - \sqrt{a^2 + b^2} &= b \\ \\ 1 - b &= \sqrt{a^2 + b^2} \\ \\ (1 - b)^2 &= a^2 + b^2 \\ \\ 1 - 2b + b^2 &= a^2 + b^2 \\ \\ 1 - 2b &= a^2 \\ \\ 2b &= 1 - a^2 \\ \\ b &= \frac{1 - a^2}{2} \\ \end{align}
So, our boundary curve has the equation \(\boxed{f(x) = \frac{1 - x^2}{2}}\), for \(-1 \leq x \leq 1\).
Graphically, this is illustrated as follows:
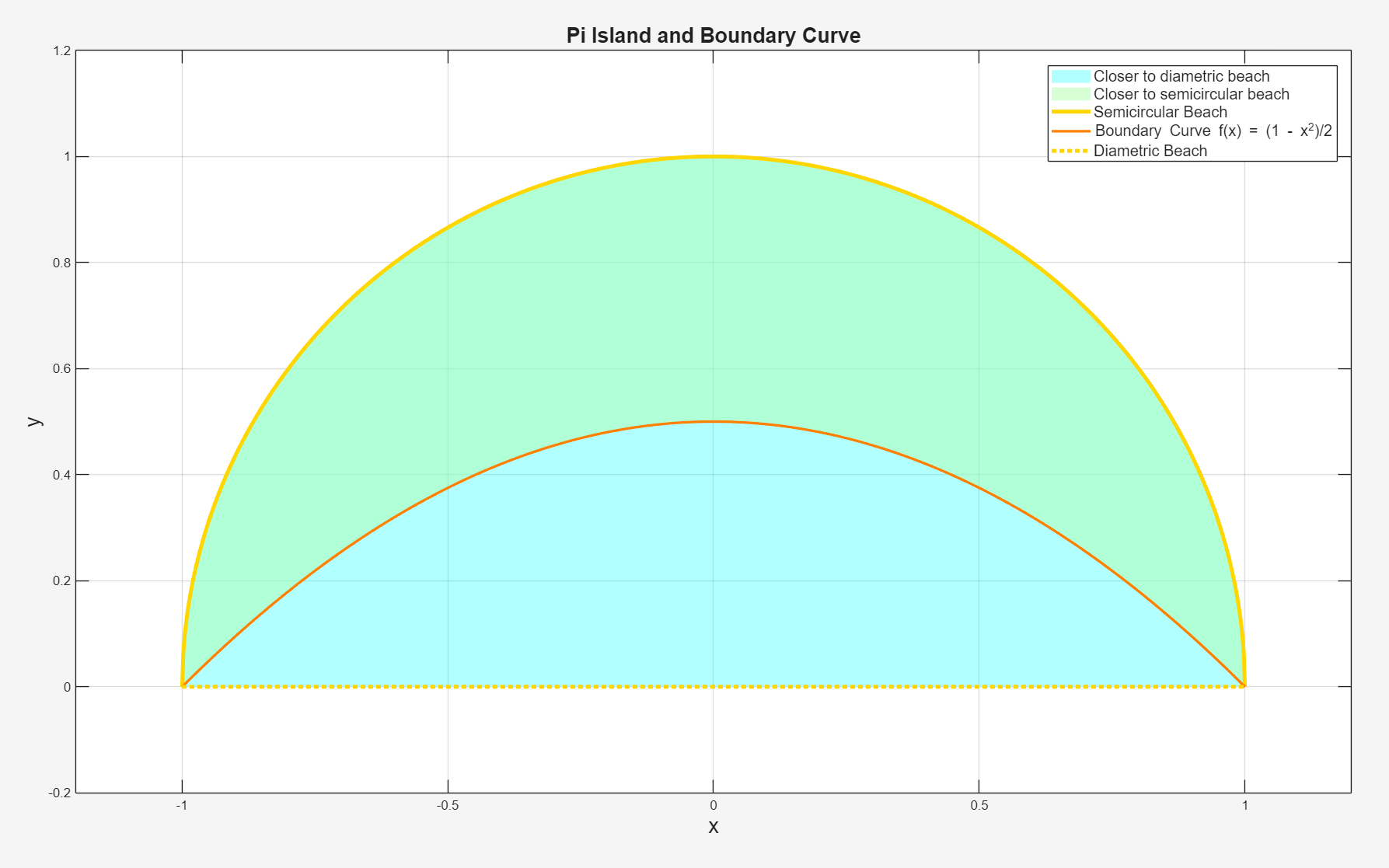
Alright, so now, we just pull in integral calculus to find the area of the blue region, as follows:
\begin{align} \text{Blue Area} &= \int_{-1}^{1} \frac{1 - x^2}{2} \; \mathrm{d}x \\ \\ &= \left.\frac{x - x^3/3}{2} \right|_{x = -1}^{x = 1} \\ \\ &= \frac{2}{3} \end{align}
So, our final answer is:
\begin{align} &\text{Probability of being closer to Diametric Beach} \\ \\ &= \frac{2/3}{\pi/2} \\ \\ &= \boxed{\frac{4}{3\pi}} \\ \\ &\approx 0.424 \\ \end{align}
If you liked using calculus in the original puzzle, you are going to love it now, as we are going turbo-speed on it. Now, average distance to boundary of a continuous area is simply the integral of the distance function over that area divided by the area itself. Recall from the original puzzle that the shortest distance is:
\begin{align} \text{shortest distance to shore} &= \min{\left(y, \; 1 - \sqrt{x^2 + y^2}\right)} \\ \end{align}
This means that we have to break the distance function into two parts: the blue region and the green region, where the colors correspond to the area in the earlier diagram.
\begin{align} &\text{Blue Region's Average Distance to Shore (To Diametric Beach)} \\ \\ &= \frac{1}{\text{Blue Region's Area}}\int_{-1}^{1} \int_{0}^{\frac{1-x^2}{2}} y \; \mathrm{d}y \, \mathrm{d}x \\ \\ &= \frac{3}{2}\int_{-1}^{1} \left.\frac{y^2}{2}\right|_{x = 0}^{x = \frac{1-x^2}{2}} \; \mathrm{d}x \\ \\ &= \frac{3}{16}\int_{-1}^{1} (1 - 2x^2 + x^4) \; \mathrm{d}x \\ \\ &= \frac{3}{16} \left(\left. x - \frac{2x^3}{3} + \frac{x^5}{5} \right|_{x = -1}^{x = 1}\right) \\ \\ &= \frac{3}{8} \left(\frac{1}{3} + \frac{1}{5}\right) \\ \\ &= \frac{1}{5} = 0.2 \text{ miles} \end{align}
That wasn't too bad! Now let's do the green region:
\begin{align} &\text{Green Region's Average Distance to Shore (To Semicircular Beach)} \\ \\ &= \frac{1}{\text{Green Region's Area}}\int_{-1}^{1} \int_{\frac{1-x^2}{2}}^{\sqrt{1 - x^2}} \left[1 - \sqrt{x^2 + y^2}\right] \; \mathrm{d}y \, \mathrm{d}x \\ \\ &= \frac{1}{\frac{\pi}{2} - \frac{2}{3}}\int_{-1}^{1} \int_{\frac{1-x^2}{2}}^{\sqrt{1 - x^2}} \left[1 - \sqrt{x^2 + y^2}\right] \; \mathrm{d}y \, \mathrm{d}x \\ \end{align}
Okay, this looks to be a lot worse than the blue region calculations, so I will resort to Wolfram Alpha.


So, the average distance to shore in the green region is approximately \(0.185862\) miles.
March 17 Update: There is a way to figure out the exact solution to the green region's average distance to semicircular beach. The idea is to use polar co-ordinates as follows.
\begin{align} x &= r \cos{\theta} \\ \\ y &= r \sin{\theta} \\ \\ \mathrm{d}y \, \mathrm{d}x &= r \, \mathrm{d}r \, \mathrm{d}\theta \\ \\ -1 \leq x \leq 1 &\Rightarrow 0 \leq \theta \leq \pi \\ \\ \frac{1-x^2}{2} \leq y \leq \sqrt{1 - x^2} &\Rightarrow \frac{1}{\sin{\theta} + 1} \leq r \leq 1 \\ \end{align}
Regarding the last line, we have the upper boundary of \(r\) being the edge of the semi-circular arc, which always has \(r = 1\). As for the lower bound, it's our boundary curve, where:
\begin{align} 1 - \sqrt{x^2 + y^2} &= y \\ \\ 1 - r &= r \sin{\theta} \\ \\ 1 &= r \sin{\theta} + r \\ \\ 1 &= r\,(\sin{\theta} + 1) \\ \\ r &= \frac{1}{\sin{\theta} + 1} \\ \end{align}
Therefore, we have:
\begin{align} &\text{Green Region's Average Distance to Shore (To Semicircular Beach)} \\ \\ &= \frac{1}{\frac{\pi}{2} - \frac{2}{3}}\int_{-1}^{1} \int_{\frac{1-x^2}{2}}^{\sqrt{1 - x^2}} \left[1 - \sqrt{x^2 + y^2}\right] \; \mathrm{d}y \, \mathrm{d}x \\ \\ &= \frac{6}{3\pi - 4}\int_{0}^{\pi} \int_{\frac{1}{\sin{\theta} + 1}}^{1} \left(1 - r\right) r \; \mathrm{d}r \, \mathrm{d}\theta \\ \\ &= \frac{6}{3\pi - 4}\int_{0}^{\pi} \int_{\frac{1}{\sin{\theta} + 1}}^{1} \left(r - r^2\right) \; \mathrm{d}r \, \mathrm{d}\theta \\ \\ &= \frac{6}{3\pi - 4}\int_{0}^{\pi} \left.\left(\frac{r^2}{2} - \frac{r^3}{3}\right)\right|_{r = \frac{1}{\sin{\theta} + 1}}^{r = 1} \; \mathrm{d}\theta \\ \\ &= \frac{6}{3\pi - 4}\int_{0}^{\pi} \frac{1}{6} - \frac{1}{2(1 + \sin{\theta})^2} + \frac{1}{3(1 + \sin{\theta})^3} \; \mathrm{d}\theta \\ \\ &= \frac{6}{3\pi - 4} \left(\frac{\pi}{6} - \frac{2}{3} + \frac{14}{45}\right) \quad \text{(Courtesy of Wolfram Alpha}) \\ \\ &= \frac{6}{3\pi - 4} \left(\frac{15\pi - 32}{90}\right) \\ \\ &= \boxed{\frac{15\pi - 32}{45\pi - 60}} \approx 0.1859 \\ \end{align}
Finally, to solve the extra credit, let's take it home using probability.
\begin{align} &\text{Expected Distance to Shore} \\ \\ &= \text{Prob of Inside Blue Region} \times \text{Average Distance to Diametric Beach} \\ &+ \text{Prob of Inside Green Region} \times \text{Average Distance to Semicircular Beach} \\ \\ &= \frac{4}{3\pi} \left(\frac{1}{5}\right) + \frac{3\pi - 4}{3\pi} \left(\frac{15\pi - 32}{45\pi - 60}\right)\\ \\ &= \frac{4}{15\pi} + \frac{15\pi - 32}{45\pi} \\ \\ &= \frac{12}{45\pi} + \frac{15\pi - 32}{45\pi} \\ \\ &= \frac{15\pi - 20}{45\pi} \\ \\ &= \boxed{\frac{3\pi - 4}{9\pi}} \approx 0.192\\ \end{align}
Therefore, the final answer is \(\frac{3\pi - 4}{9\pi} \approx 0.192\) miles.
If we were on a circular island of radius \(R\), as circles are more closely related to \(\pi\), our average distance to shore would be:
\begin{align} &\text{Average Distance to Shore} \\ \\ &= \frac{1}{\pi R^2}\int_{-\pi}^{\pi} \int_{0}^{R} (1 - r) \; r \, \mathrm{d}r \, \mathrm{d}\theta \\ \\ &= \frac{2\pi}{\pi R^2}\int_{0}^{R} (r - r^2) \; \mathrm{d}r \\ \\ &= \frac{2}{R^2} \left.\left(\frac{r^2}{2} - \frac{r^3}{3}\right) \right|_{0}^{R} \\ \\ &= \frac{2}{R} \left(\frac{R^2}{2} - \frac{R^3}{3}\right) \\ \\ &= \boxed{R - \frac{2R^2}{3}} \\ \end{align}
Again, we integrate the distance function, \((1 - r)\), over the area of the circle and divide by the area itself. Here, we are working with polar co-ordinates as we don't have to worry about the pesky straightline diameter anymore.
If \(R = 1\), then our average distance to shore would be \(1 - \frac{2}{3} = \frac{1}{3}\).