



December 3, 2024
I am inspired by the latest video from YouTube science content creator Veritasium on rainbows. Yes, rainbows. What struck me the most about his video is how he explained the way rainbows appear in the sky. The short answer we are all accustomed to hearing is that each raindrop acts as a prism that diffracts sunlight. However, if that is the case, why can't we ever see a rainbow while facing towards the sun?
The proper answer, summarised here from the video, is that the rainbow is a culmination of the diffraction patterns of each individual raindrop. As sunlight enters a raindrop, which is spherical, the light ray refracts going into the spherical drop, reflects at the back of the raindrop, before traveling out of the raindrop while refracting once more. For the light rays hitting the spherical drop near the central diameter of the sphere, the refraction angle is very tiny, and so there isn't much difference in the paths of light rays among the different frequencies of light, and the output light ray is the overlapping of each frequency, and you see white light. However, there are certain rays entering the raindrop such that the angle between the output refracted ray and the incident ray is at a maximum, which is around 42 degrees. In this case, the differences among the paths of different frequencies of the white light is tangible enough that we see the white light diffracted, hence the rainbow. In addition, since the output refracted ray is coming out of the front of the raindrop, you have to face away from the sun in order to observe it.
The following diagram illustrates the light ray's path going through a single raindrop, which is modeled here as a unit circle:
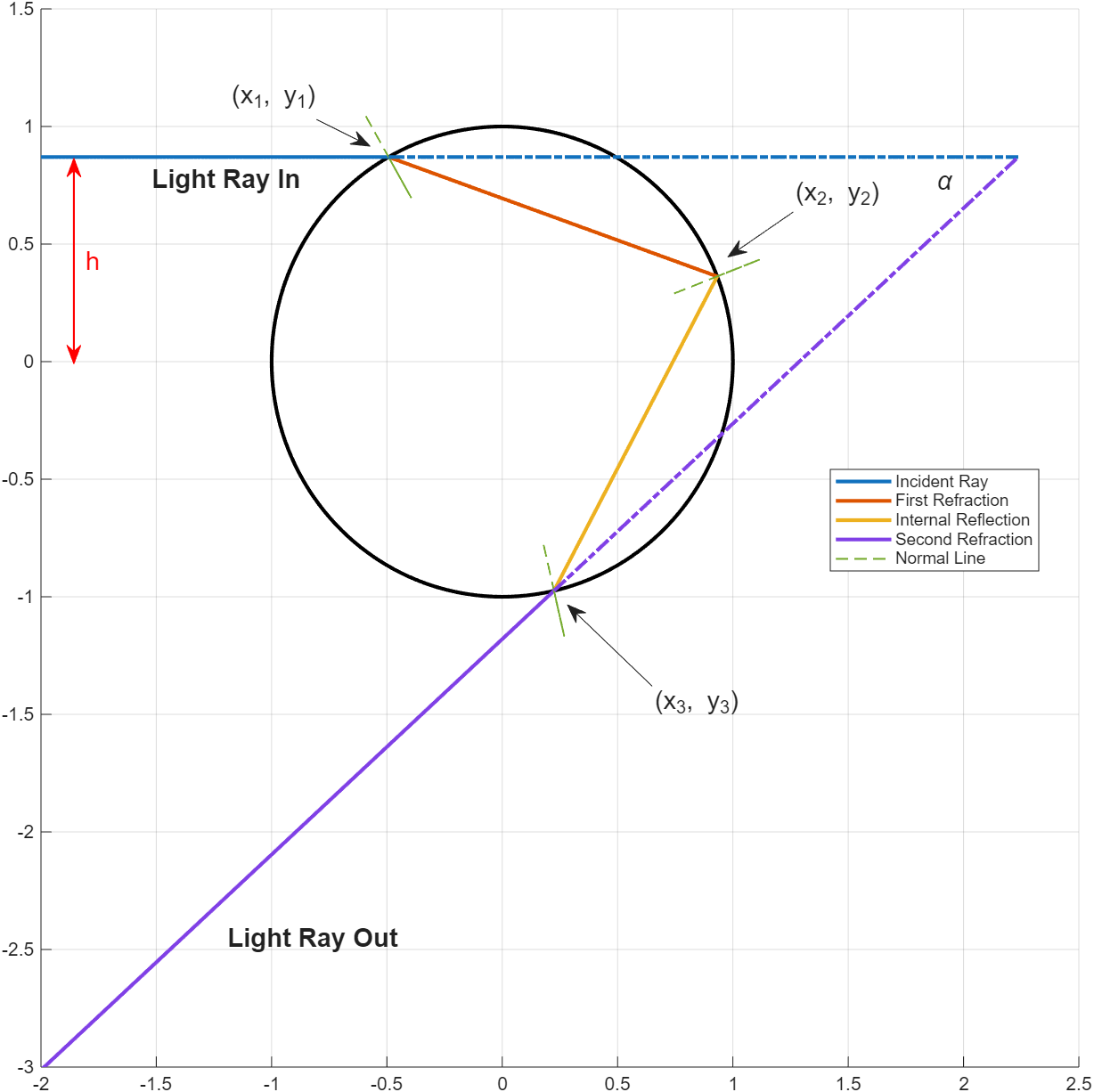
The following plot shows the changing of the angle between the output refracted ray and the incident ray (\(\alpha\)) against \(h\), which is the height in which the light ray is entering the spherical rain drop.
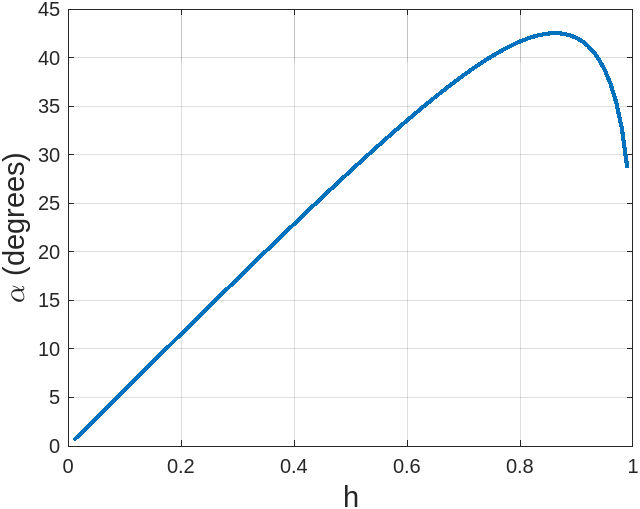
As one can see, the maximum angle is around 42 degrees, which is achieved when the light ray enters the spherical raindrop about 7/8th of the radius of the sphere above the center (0.875).
I made an interactive MATLAB app to investigate the different light paths as \(h\) changes. Demo video is shown as below:
As for the actual interactive app, please click here to open it on MATLAB Online!
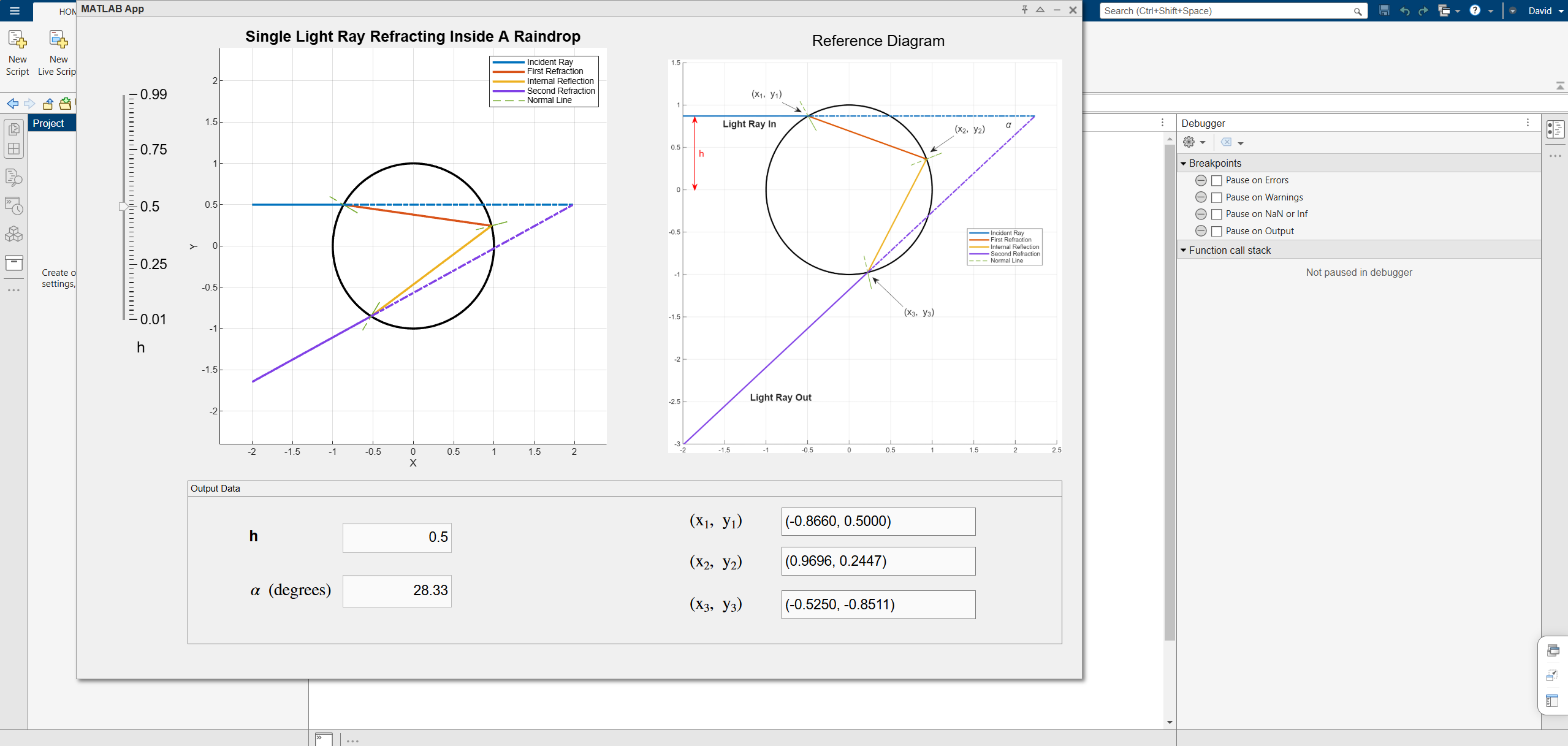
Alternatively, you can use this link to open the app install file on MATLAB Online (free of charge). Once opened, click on the "Rainbow Simulator.mlappinstall" file and follow the instructions to install and see the Rainbow Simulator app on the "Apps" tab!
All source code can be found in my Github repo:
https://github.com/dvfire123/RainbowSimulator/tree/main
***
Finally, here is the awesome rainbow video by Veritasium: