



December 25, 2023
I have a task for you. I want you to take the following infinite series:
\begin{align} \sum_{n = 1}^{\infty} \frac{1}{n} &= 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots \\ \end{align}
And turn it into one. Yes, the number "1". Here's the catch though: you cannot just say, "let me take away every term after the first one". No. Instead, you need to provide for me a systematic way of doing so, namely, a series of steps where in each step, I follow some rule as a function of the step number, and gradually, whittle the infinite series down to just the first term, one. How would you do it?

As the title of the blog post suggests, you would use some sort of "filter" in each step to eliminate a subset of the terms, such that in all of the subsequent steps the filter would only deal with the remaining ones. Such a filter would be comprehensive enough to sift out every term other than the first "1", thereby achieving the goal. I am motivated to write about this while reminiscing about the very first crossword puzzle I published on Universal Crossword, titled "Sifting Through Things". I detailed my journey to eventually realizing my dream of publishing that crossword puzzle in my other blog post, How I Crossed Crosswords Part 3: Constructing a Crossword, so if you are interested, please feel free to give it a read! Anyways, back to this blog post. The "filter" that would prove to be quite effective here is an ancient algorithm called the "Sieve of Eratosthenes [Era-TUH-ste-nes]". It is an algorithm, known since the early 2nd century from ancient Greece, for finding prime numbers by sifting out all numbers that are some multiples of known prime numbers, as the following illustrates.
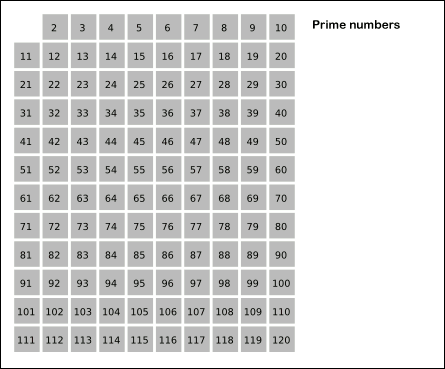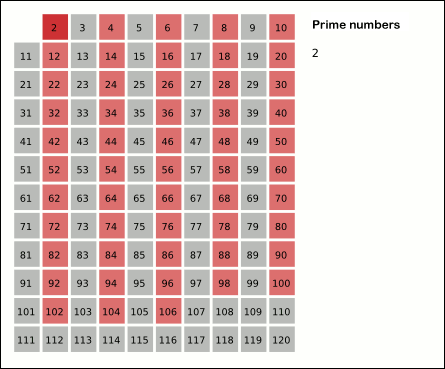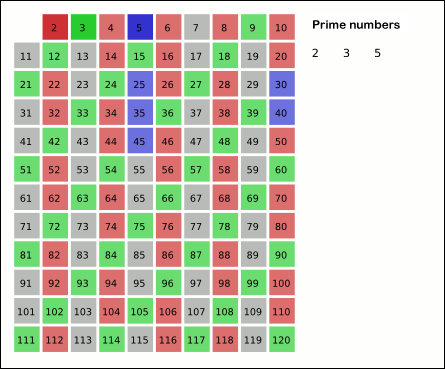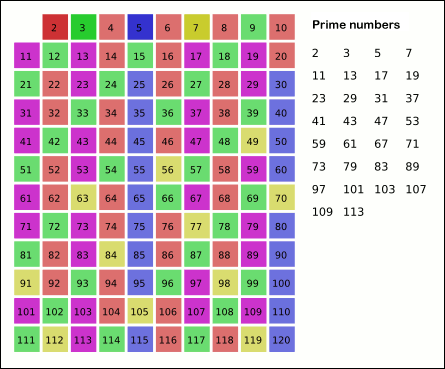
Here's how I would describe the steps to whittle down the infinite series to just "1". At step \(k\), I would strike out all the terms whose denominators are the integer multiples of the \(k\)th prime number, including the starting term. Let's see how this would work. In step 1, the first prime number is "2". Therefore, all terms whose denominators are integer multiples of 2, including 2 itself, are eliminated. This leaves us with:
\begin{align} 1 + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \frac{1}{9} + \dots \\ \end{align}
Namely, "1" and the fractions whose denominators are odd. Next, on step 2, I would strike out all terms whose denominators are the integer multiples of the second prime number, "3", including 3 itself. This means terms like \(\frac{1}{3}, \frac{1}{9}, \frac{1}{15}, \dots \) are gone, which leaves us with:
\begin{align} 1 + \frac{1}{5} + \frac{1}{7} + \frac{1}{11} + \frac{1}{13} + \frac{1}{17} + \dots \\ \end{align}
Just after two steps, you can already see that most of the fraction terms left based on the first few terms have prime denominators. What we are doing is effectively applying the Sieve of Eratosthenes to eliminate more and more terms. The next step would sift out the multiples of "5"'s, then the "7"'s, then the "11"'s, and so on.
Before we examine how many steps it takes to complete our task, let's first translate our steps into math. Consider the first step, where we want to eliminate all the multiples of "2"'s. We have:
\begin{align} & \left(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots\right) - \left(\frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \dots\right)\\ \\ &= \left(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots\right) - \left(\frac{1}{2}\right) \left(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots\right) \\ \\ &= \left(1 - \frac{1}{2}\right) \left(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots\right) \end{align}
There you have it. I did not simplify the terms in the first bracket because I want to demonstrate a pattern here. The beauty about the sieve is that we can immediately apply the subsequent steps on the resulting series from the previous sifting. For example, for step 2, where we examine the multiples of "3"'s, we have:
\begin{align} & \left(1 + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \dots\right) - \left(\frac{1}{3} + \frac{1}{9} + \frac{1}{15} + \dots\right)\\ \\ &= \left(1 + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \dots\right) - \left(\frac{1}{3}\right) \left(1 + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \dots\right) \\ \\ &= \left(1 - \frac{1}{3}\right) \left(1 + \frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \dots\right) \\ \\ &= \left(1 - \frac{1}{3}\right) \left(1 - \frac{1}{2}\right) \left(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots\right) \end{align}
Where the last line comes from the result of the sifting of the "2"'s.
This is a very elegant result because we preserve our original infinite series, and we simply multiply it by the expression \(\left(1 - \frac{1}{p_k}\right)\), where \(p_k\) is the \(k\)th prime number.
When do we stop? Well, we stop when all the numbers other than "1" are eliminated by ever-increasing \(k\)'s step by step. An interesting observation here is that this does not depend on whether or not there is an infinite number of primes or not. There could be, or there could not. We don't care. All we are concerned with is that by going over the integer multiples of the prime numbers, eventually all of the fraction terms are eliminated and we are left with the first term, "1", and hence mission accomplished!
Writing out our completed task in math-speak, we have:
\begin{align} 1 &= \left(1 - \frac{1}{p_1}\right) \left(1 - \frac{1}{p_2}\right)\dots\left(1 - \frac{1}{p_k}\right) \dots \sum_{n = 1}^{\infty} \frac{1}{n} \\ \\ \sum_{n = 1}^{\infty} \frac{1}{n} &= \left(\frac{1}{1 - p_1^{-1}}\right) \left(\frac{1}{1 - p_2^{-1}}\right)\dots\left(\frac{1}{1 - p_k^{-1}}\right) \dots \\ \\ \end{align}
Remember, \(p_k\) is the \(k\)th prime number. E.g. \(p_1 = 2\) and \(p_2 = 3\).
The re-written line is a special case of the "Euler product", which connects prime numbers with a very peculiar function that I will talk about later.
Remember how the above filtering did not care about whether the number of primes is infinite or not? We can use the result to prove that the number of primes is, in fact, infinite. Euler himself proved it using proof by contradiction, along the lines of the factorial of the largest prime + 1 must be a prime number. However, here, we can prove it directly. All we have to show is that the left-hand side, namely our infinite series, which is called the "harmonic series", is infinite. We can use lower bounds:
\begin{align} \sum_{n = 1}^{\infty} \frac{1}{n} &= 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \dots \\ \\ &\ge \frac{1}{2} + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \dots \\ \\ &= 1 + \sum_{n = 3}^{\infty} \frac{1}{2^{\lceil \log_2{n} \rceil}} \\ \\ &= 1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \dots \\ \\ &= \infty \end{align}
Therefore, the harmonic series is divergent. By the Euler product, it is also equal to the product of a finite expression involving ever-increasing prime numbers, namely \(\left(\frac{p_k}{p_k - 1}\right)\), the number of primes must be infinite, otherwise the product on the right-hand side of the Euler product equation would be a finite product. So in fact, our filtering process would have infinite steps, and the limiting result is the number "1".
Our Euler product actually has a general form:
\begin{align} \sum_{n = 1}^{\infty} \frac{1}{n^s} &= \left(\frac{1}{1 - p_1^{-s}}\right) \left(\frac{1}{1 - p_2^{-s}}\right)\dots\left(\frac{1}{1 - p_k^{-s}}\right) \dots \\ \end{align}
Or written more concisely:
\begin{align} \sum_{n = 1}^{\infty} \frac{1}{n^s} &= \prod_{k = 1}^{\infty} \left(\frac{1}{1 - p_k^{-s}}\right) \\ \end{align}
The generalization is the introduction of the parameter "s". In our harmonic series case, "s" is simply "1". However, for any other values of "s", including complex numbers, the Euler product identity holds. This means if you were reading my earlier blog post about going pie hunting, you would've come across this:
\begin{align} \frac{\pi^2}{6} &= \sum_{n = 1}^{\infty} \frac{1}{n^2} \\ \\ &= \prod_{k = 1}^{\infty} \left(\frac{1}{1 - p_k^{-2}}\right) \\ \\ &= \left(\frac{p_1^2}{p_1^2 - 1}\right) \left(\frac{p_2^2}{p_2^2 - 1}\right) \left(\frac{p_3^2}{p_3^2 - 1}\right) \dots \\ \\ &= \left(\frac{2^2}{2^2 - 1}\right) \left(\frac{3^2}{3^2 - 1}\right) \left(\frac{5^2}{5^2 - 1}\right) \dots \\ \end{align}
Yes, we just connected \(\pi\) with prime numbers.

***
Conveniently, the left-hand side of the Euler's product in the generalized form is a well-known function, called the Riemann zeta function. It is a function of "s" ("n" is just a dummy variable used to iterate the terms of the series), where "s" is a complex number in general, and the output of the function is also a complex number in general. We denote the function using the Greek letter "zeta":
\begin{align} \zeta(s) &= \sum_{n = 1}^{\infty} \frac{1}{n^s} \\ \end{align}
The above function is the Riemann zeta function, and the expression converges when the real part of "s" is greater than 1. When it is less than or equal to one, we, and by "we", I mean the complex analysts, use a technique called "analytic continuation" to bring the function to map over all complex values.
It turns out that after performing analytical continuation, \(\zeta(-1) = -\frac{1}{12}\), which is the root of the running math joke that \(1 + 2 + 3 + 4 + 5 + \dots = -\frac{1}{12}\). Also, all negative even integer values of "s" will have \(\zeta(s) = 0\). They are called the "trivial zeros of the Riemann zeta function". It has been proven that all non-trivial zeros lie in the complex plane for which the real part of s is between 0 and 1. This is called the "critical strip". Furthermore, all known non-trivial zeros of the Riemann zeta function has been observed to have the real part \(\frac{1}{2}\). Therefore, the line "real(s) = 1/2" is called the critical line. It has been hypothesized that ALL non-trivial zeros lie on this line. If you can prove this hypothesis, called the "Riemann Hypothesis", there is a one million dollar prize waiting for you to claim. One such non-trivial zero is (1/2 ± 14.134725i). Good luck!