



February 14, 2025
Here is a fun Valentine's day puzzle for all of the math enthusiasts out there, courtesy of Fiddler on the Proof:
You can generate a heart shape by drawing a unit square (i.e., a square with side length 1), and then attaching semicircles (each with radius 1/2) to adjacent edges, as shown in the diagram below:

What is the radius of the smallest circle that contains this heart shape?
Alright, give it some thought. When you are ready, see the answer below!
*** SPOILER ALERT! ***
Solution:
The gist of the solution is illustrated as below. I will explain the steps in detail. Here, we let the radius of the big circle be \(r\).
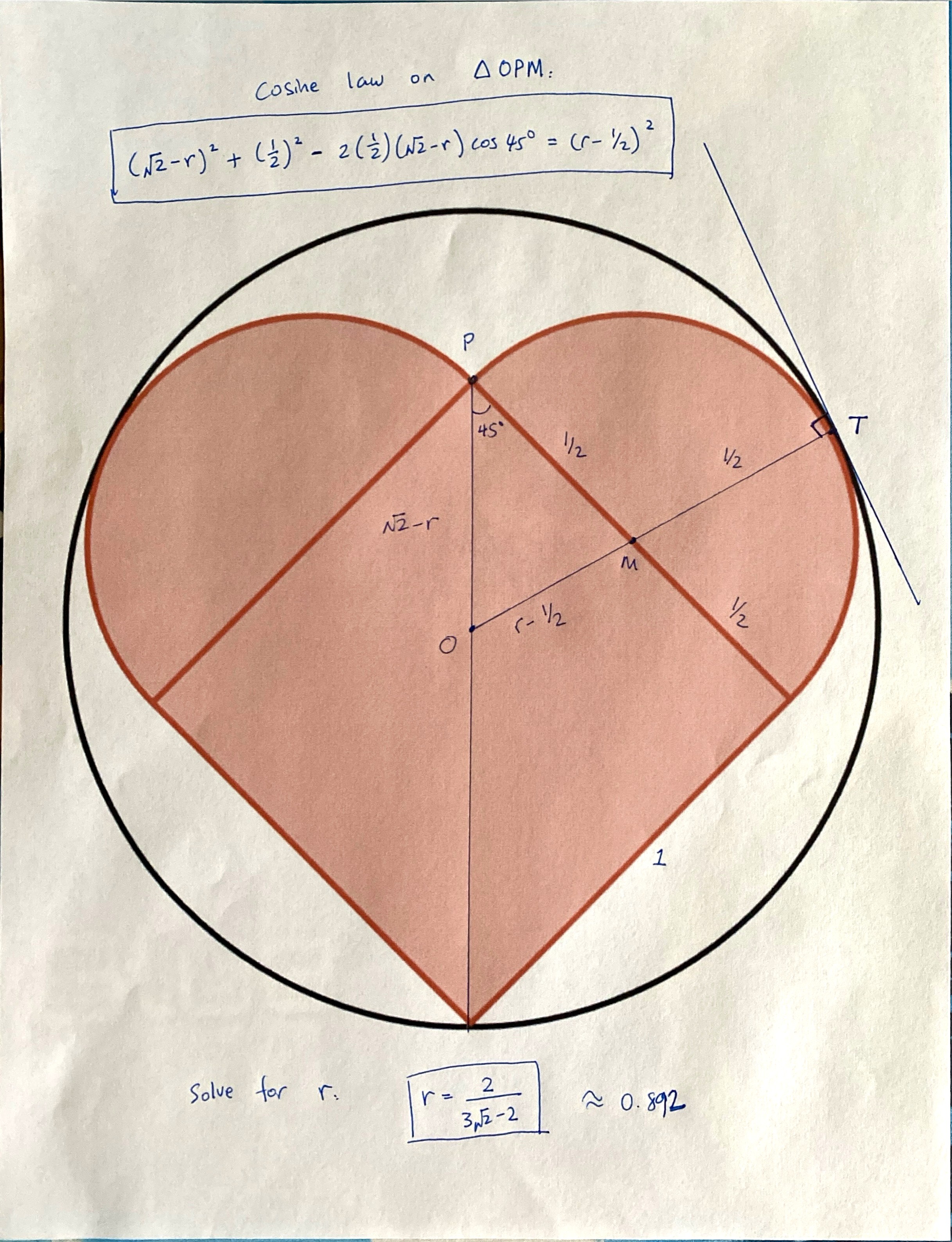
First, by symmetry, we know that the center of the big circle lies somewhere on the main diagonal of the unit square. Let that point be O. Then, since the big circle is to be as small as possible, it will need to be tangent to each of the two semi-circles. Let T be the common tangent point between the big circle and the right semi-circle. Now, the tangent line is always perpendicular to the line segment connecting the tangent point to the center of the circle. Therefore, MT and OT are co-linear. This gives rise to the fact that OM has length (\(r - 1/2\)). Also, since MP is a radius of the semi-circle, it has length \(1/2\).
Next, the length of the main diagonal of the unit square is \(\sqrt{2}\). Since we let the radius of the big circle having radius \(r\), this means that OP has length (\(\sqrt{2} - r\)).
Then, we note that since OP lies along the main diagonal of the unit square, angle OPM is 45 degrees.
Finally, we have all the information we need to apply the Cosine Law on triangle OPM, as follows:
\begin{align} (\sqrt{2} - r)^2 + \left(\frac{1}{2}\right)^2 - 2\left(\frac{1}{2}\right)(\sqrt{2} - r)\cos{45^o} &= \left(r - \frac{1}{2}\right)^2 \\ \\ (\sqrt{2} - r)^2 + \left(\frac{1}{2}\right)^2 - 2\left(\frac{1}{2}\right)(\sqrt{2} - r)\left(\frac{\sqrt{2}}{2}\right) &= \left(r - \frac{1}{2}\right)^2 \\ \\ 2 - 2\sqrt{2}r + r^2 + \frac{1}{4} - 1 + \frac{\sqrt{2}}{2} r &= r^2 - r + \frac{1}{4} \\ \\ 2\sqrt{2}r - \frac{\sqrt{2}}{2} r - r &= 1 \\ \\ \left(\frac{3\sqrt{2}}{2} - 1\right) r &= 1 \\ \\ r = \frac{1}{\frac{3\sqrt{2}}{2} - 1}&\\ \\ r = \frac{2}{3\sqrt{2} - 2} &= \boxed{\frac{3\sqrt{2} + 2}{7}} \approx 0.892 \\ \end{align}
We can do a sanity check to see that \(r > \frac{\sqrt{2}}{2} \approx 0.707\), since the diameter of the big circle needs to be greater than the main diagonal of the unit square, which is \(\sqrt{2}\).
Happy Valentine's Day!