



Jan 10, 2025
Fiddler answer: \(N = 454\)
Extra Credit: \(N = 359\)
Explanation:
For the first Fiddler, I wrote MATLAB code to help find the smallest \(N\). The code is as below:
function [survive, elim, numGroups] = playMingleOneRound(N, k)
% Play one round of Mingle with N players and the target group size is
% k. Output number of survivals in "survive" and number of eliminated
% in "elim". Also output number of groups formed by surviving players.
numGroups = floor(N/k);
survive = k * numGroups;
elim = N - survive;
end
function res = atLeastOneSurvived(N)
% Function to find out if at least one survivor in Mingle after 38
% rounds for N players. Returns true if so and false otherwise.
rounds = 1:38;
survive = N;
for k = rounds
survive = playMingleOneRound(survive, k);
if survive == 0
res = false;
return;
end
end
res = true;
end
%% Main script to find smallest N such that at least one survivor after 38 rounds of Mingling
N = 38; % We need at least 38 players otherwise everyone is elminated in round 38
res = false;
while res == false
fprintf('Analyzing N = %d...\n', N)
res = atLeastOneSurvived(N);
if res == true
break;
end
N = N + 1;
end
fprintf('Found smallest N = %d\n', N);
Here is the output:
Found smallest N = 454
So, it turns out that the smallest \(N\) is 454.
For completeness, I also printed out the Mingle process for 454 players, showing that 38 players survive after 38 rounds:
Round: 1; Survived: 454; Eliminated: 0; Number of groups: 454 Round: 2; Survived: 454; Eliminated: 0; Number of groups: 227 Round: 3; Survived: 453; Eliminated: 1; Number of groups: 151 Round: 4; Survived: 452; Eliminated: 1; Number of groups: 113 Round: 5; Survived: 450; Eliminated: 2; Number of groups: 90 Round: 6; Survived: 450; Eliminated: 0; Number of groups: 75 Round: 7; Survived: 448; Eliminated: 2; Number of groups: 64 Round: 8; Survived: 448; Eliminated: 0; Number of groups: 56 Round: 9; Survived: 441; Eliminated: 7; Number of groups: 49 Round: 10; Survived: 440; Eliminated: 1; Number of groups: 44 Round: 11; Survived: 440; Eliminated: 0; Number of groups: 40 Round: 12; Survived: 432; Eliminated: 8; Number of groups: 36 Round: 13; Survived: 429; Eliminated: 3; Number of groups: 33 Round: 14; Survived: 420; Eliminated: 9; Number of groups: 30 Round: 15; Survived: 420; Eliminated: 0; Number of groups: 28 Round: 16; Survived: 416; Eliminated: 4; Number of groups: 26 Round: 17; Survived: 408; Eliminated: 8; Number of groups: 24 Round: 18; Survived: 396; Eliminated: 12; Number of groups: 22 Round: 19; Survived: 380; Eliminated: 16; Number of groups: 20 Round: 20; Survived: 380; Eliminated: 0; Number of groups: 19 Round: 21; Survived: 378; Eliminated: 2; Number of groups: 18 Round: 22; Survived: 374; Eliminated: 4; Number of groups: 17 Round: 23; Survived: 368; Eliminated: 6; Number of groups: 16 Round: 24; Survived: 360; Eliminated: 8; Number of groups: 15 Round: 25; Survived: 350; Eliminated: 10; Number of groups: 14 Round: 26; Survived: 338; Eliminated: 12; Number of groups: 13 Round: 27; Survived: 324; Eliminated: 14; Number of groups: 12 Round: 28; Survived: 308; Eliminated: 16; Number of groups: 11 Round: 29; Survived: 290; Eliminated: 18; Number of groups: 10 Round: 30; Survived: 270; Eliminated: 20; Number of groups: 9 Round: 31; Survived: 248; Eliminated: 22; Number of groups: 8 Round: 32; Survived: 224; Eliminated: 24; Number of groups: 7 Round: 33; Survived: 198; Eliminated: 26; Number of groups: 6 Round: 34; Survived: 170; Eliminated: 28; Number of groups: 5 Round: 35; Survived: 140; Eliminated: 30; Number of groups: 4 Round: 36; Survived: 108; Eliminated: 32; Number of groups: 3 Round: 37; Survived: 74; Eliminated: 34; Number of groups: 2 Round: 38; Survived: 38; Eliminated: 36; Number of groups: 1
The more interesting problem is in the Extra Credit. At first glance, this might seem impossible to solve, or at least, very complicated. However, with a few observations, we can solve the problem indirectly without calculating the expected values of every \(N\) up to 499. Here's how.
First, note the geometric distribution, which states that if we perform an independent trial with each trial having a \(p\) chance of success, then the expected number of trials we need before getting a successful trial, including the successful trial itself, is \(1/p\). This can be seen when \(N = 1\). The expected number of rounds is \(10/9\), since the "success" here is getting \(k\) to be called 2 through 10, which has a \(9/10\) chance of happening. Once a number other than 1 is called, that round is the last round as everyone, i.e. the lone player, will be eliminated afterwards since a single player cannot form groups of greater than 1.
Second, with \(N\) players, note that the game is memoryless. That is, once \(N\) is whittled down to a smaller number, \(M\), then the expected number of rounds with \(M\) players is independent of how we got to \(M\) players from \(N\) players.
Third, note that the question asks the value of \(N\) such that \(N + 1\) has 10 more rounds, on average. We don't need to figure out the expected rounds with \(N\) players, just a scenario where the expected number of rounds jumps by 10 more rounds as soon as we add one more player.
That means, we need a number \(N + 1\) such that nine out of ten times (as numbers 1 through 10 are the possible group sizes) the total player size remains the same, and the one time where the total player size decreases. We also have the constraint that \(N < 500\).
The only way that the total player size remains the same after a round is if the group size, \(k\) evenly divides the player size. Since we require nine out of the ten numbers 1 through 10 to evenly divide that number, we need to be methodical about it. The least common multiple of a group of numbers increases most dramatically if we include a prime number, since we must multiply the previous LCM by that prime number as that number cannot be divided further. Among the numbers 1 through 10, 7 is the largest prime number. We can also check that numbers 8, 9, 10 all have factors less than 7 other than the numbers themselves. Since there is a size constraint of \(N < 500\), let's exclude 7. So, what is the LCM of 1, 2, 3, 4, 5, 6, 8, 9, 10? The answer is 360, a number that is less than 500.
Another methodical way to show that \(N + 1 = 360\) is the ONLY solution for \(N < 500\) is to lay out the prime factorizations of 2 through 10. We have:
\(2 = 2\)
\(3 = 3\)
\(4 = 2^2\)
\(5 = 5\)
\(6 = 2 \times 3\)
\(7 = 7\)
\(8 = 2^3\)
\(9 = 3^2\)
\(10 = 2 \times 5\)
The LCM of any set of numbers is the product of the highest powers of primes found in the prime factorizations of those numbers. Since 7 is prime, any other set of numbers 1 through 10 excluding a number would mean that we need to multiply back 7 and divide by any prime powers that we no longer need. As \(360 * 7 = 2520 > 500\), we need a big division to have a second possible \(N + 1\). Let's take a look:
Excluding 2 changes nothing, as 4 and 8 are all higher powers of 2. Excluding 3 also changes nothing as 9 is a higher power of 3. Same line of thinking applies to 4. For 5, as 10 is a multiple of 5, this also changes nothing. Same applies to 6 as well (6 = 2 times 3). For 8, once we elimiate it, we can divide 2520 by 2 as we don't need a third power of 2 anymore. However, (2520/2 = 1260 > 500). For 9, we can divide 2520 by 3 but (2520/3 = 840 > 500). Finally, for 10, if we exclude it instead of 7, we just need to divide 2520 by 2 but that's 1260 > 500.
Therefore, we can only exclude 7 to have a number for the total player size, i.e. 360, to have a 9/10 chance of remaining the same and a 1/10 chance of decreasing, thereby extending the expected number of rounds played by 10 than the previous number, which is what the problem is asking.
I also confirmed this with Monte-Carlo simulation of 100,000 trials for each player size ranging from 1 to 499 (note the big jump around \(N = 359\)):
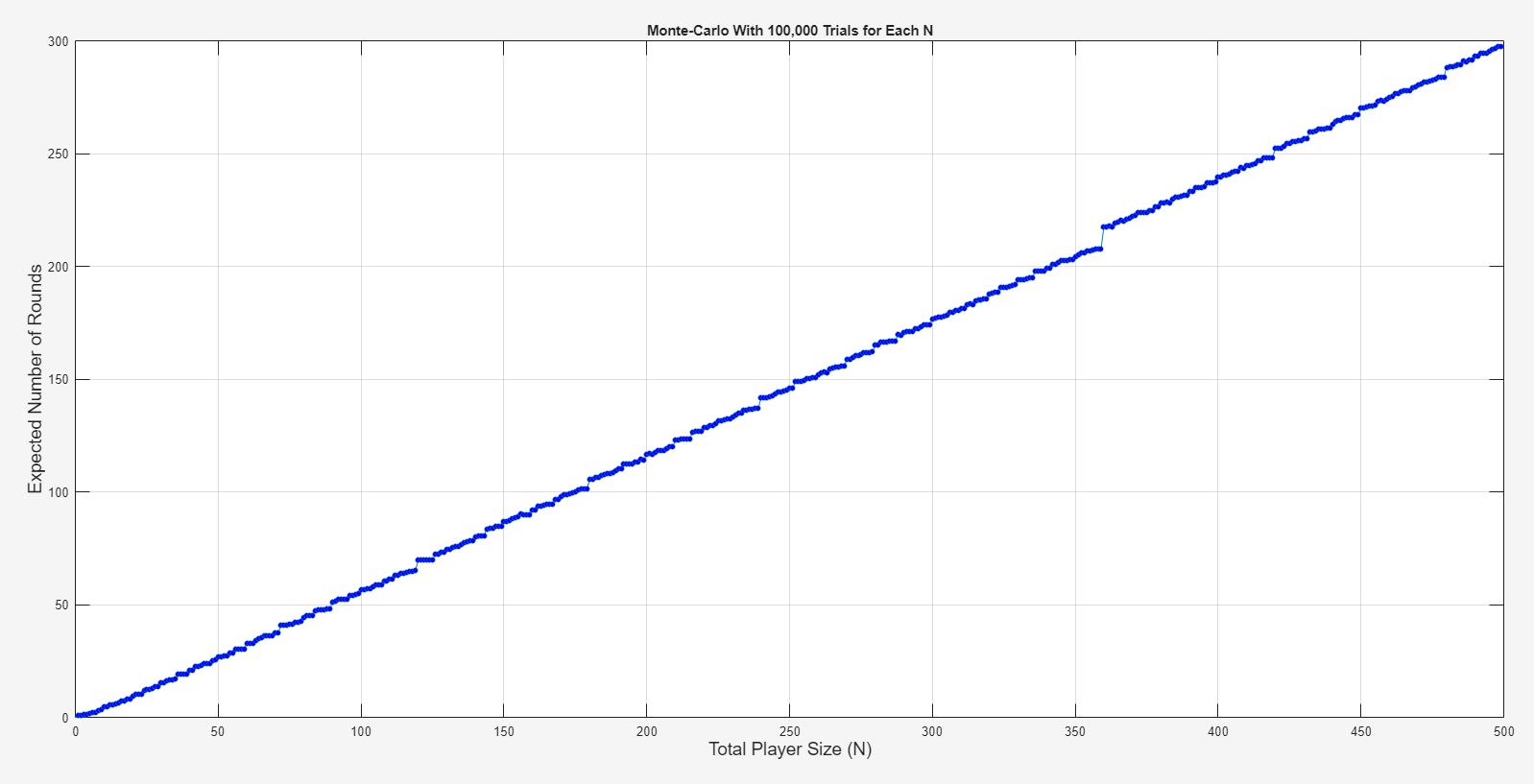
Therefore, the answer is \(N = 359\).