



Jan 24, 2025
Fiddler answer: \(\frac{3}{5} = 0.6\)
Extra Credit: \(\frac{e - 1}{e} \approx 0.63\)
Explanation:
It is more efficient to analyze both puzzles at once by analyzing the general problem: instead of 4 lily pads, what if there are \(N\) lily pads? For the original puzzle, \(N = 4\), and for the extra credit, \(N \to \infty\).
Let \(p_k\) represent the probability that the frog eventually jumps to lily pad 1 starting on lily pad \(k\). In our general setup, \(p_1 = 1\) and \(p_N = 0\). For \(2 \leq k \leq N-1\), we have the following relationship from the puzzle's given:
\begin{align} p_k &= \frac{1}{k} p_{k-1} + \frac{k - 1}{k} p_{k+1} \\ \end{align}
Now, let us re-arrange the above equation to get a difference equation. This will give us opportunities to "telescope" series later on, which will greatly simply analysis.
\begin{align} p_k &= \frac{1}{k} p_{k-1} + \frac{k - 1}{k} p_{k+1} \\ \\ k p_k &= p_{k-1} + (k - 1)p_{k + 1} \\ \\ (k - 1) p_k + p_k &= p_{k-1} + (k - 1)p_{k + 1} \\ \\ p_k - p_{k-1} &= (k - 1)(p_{k + 1} - p_k) \\ \\ p_{k + 1} - p_k &= \frac{p_k - p_{k-1}}{k - 1} \\ \end{align}
Bringing one of the boundary conditions, namely \(p_1 = 1\), into the above difference equation, and we have:
\begin{align} p_{k + 1} - p_k &= \frac{p_k - p_{k-1}}{k - 1} \\ \\ p_3 - p_2 &= \frac{p_2 - p_1}{k - 1} = \frac{p_2 - 1}{1} \\ \\ p_4 - p_3 &= \frac{p_3 - p_2}{k - 1} = \frac{p_3 - p_2}{2} = \frac{p_2 - 1}{2 \times 1} \\ \\ p_5 - p_4 &= \frac{p_4 - p_3}{k - 1} = \frac{p_4 - p_3}{3} = \frac{p_2 - 1}{3 \times 2 \times 1} \\ \\ &\dots \\ \\ p_k - p_{k - 1} &= \frac{p_2 - 1}{(k - 2)!} \\ \\ &\dots \\ \\ p_N - p_{N - 1} &= \frac{p_2 - 1}{(N - 2)!} \end{align}
Thanks to telescoping, we can arrive at any \(p_k\) using our difference equation by expressing the following:
\begin{align} p_k - p_1 &= (p_k - p_{k-1}) + (p_{k - 1} - p_{k-2}) + \dots + (p_2 - p_1) \end{align}
For which we know that \(p_1\) = 1 and \(p_k - p_{k-1} = \frac{p_2 - 1}{(k - 2)!}\) for \(2 \leq k \leq N - 1\). Now, to figure out a closed form expression for \(p_2\), we just need to bring in the other boundary condition, \(p_N = 0\).
\begin{align} p_N - p_1 &= \sum_{i = 2}^{N} (p_i - p_{i-1}) \\ \\ 0 - 1 &= \sum_{i = 2}^{N} \frac{p_2 - 1}{(i - 2)!} \\ \\ -1 &= (p_2 - 1)\sum_{i = 2}^{N} \frac{1}{(i - 2)!} \\ \\ p_2 - 1 &= - \frac{1}{\sum_{i = 2}^{N} \frac{1}{(i - 2)!}}\\ \\ p_2 &= 1 - \frac{1}{\sum_{i = 2}^{N} \frac{1}{(i - 2)!}} \end{align}
So, the closed form expression for \(p_2\) is:
\begin{align} \boxed{p_2 = 1 - \frac{1}{\sum_{i = 2}^{N} \frac{1}{(i - 2)!}}} \end{align}
For the original puzzle, \(N = 4\), and so:
\begin{align} p_2 &= 1 - \frac{1}{\sum_{i = 2}^{N} \frac{1}{(i - 2)!}} \\ &= 1 - \frac{1}{\sum_{i = 2}^{4} \frac{1}{(i - 2)!}} \\ \\ &= 1 - \frac{1}{1/0! + 1/1! + 1/2!} \\ \\ &= 1 - \frac{1}{5/2}\\ \\ &= 1 - \frac{2}{5} \\ \\ p_2 &= \boxed{\frac{3}{5}} = 0.6 \end{align}
For the extra credit, we let \(N \to \infty\):
\begin{align} p_2 &= \lim_{N \to \infty} 1 - \frac{1}{\sum_{i = 2}^{N} \frac{1}{(i - 2)!}} \\ \\ &= \lim_{N \to \infty} 1 - \frac{1}{\sum_{k = 0}^{N-2} \frac{1}{k!}} \\ \\ &= 1 - \frac{1}{\sum_{k = 0}^{\infty} \frac{1}{k!}} \\ \\ &= 1 - \frac{1}{e} \quad \text{(Maclaurin series expansion of the exponential function)}\\ \\ p_2 &= \boxed{\frac{e - 1}{e}} \approx 0.63\\ \\ \end{align}
Below is a graph of Monte-Carlo simulation of 100,000 trials vs theory for \(p_2\) over different values of \(N\) (on a log scale).
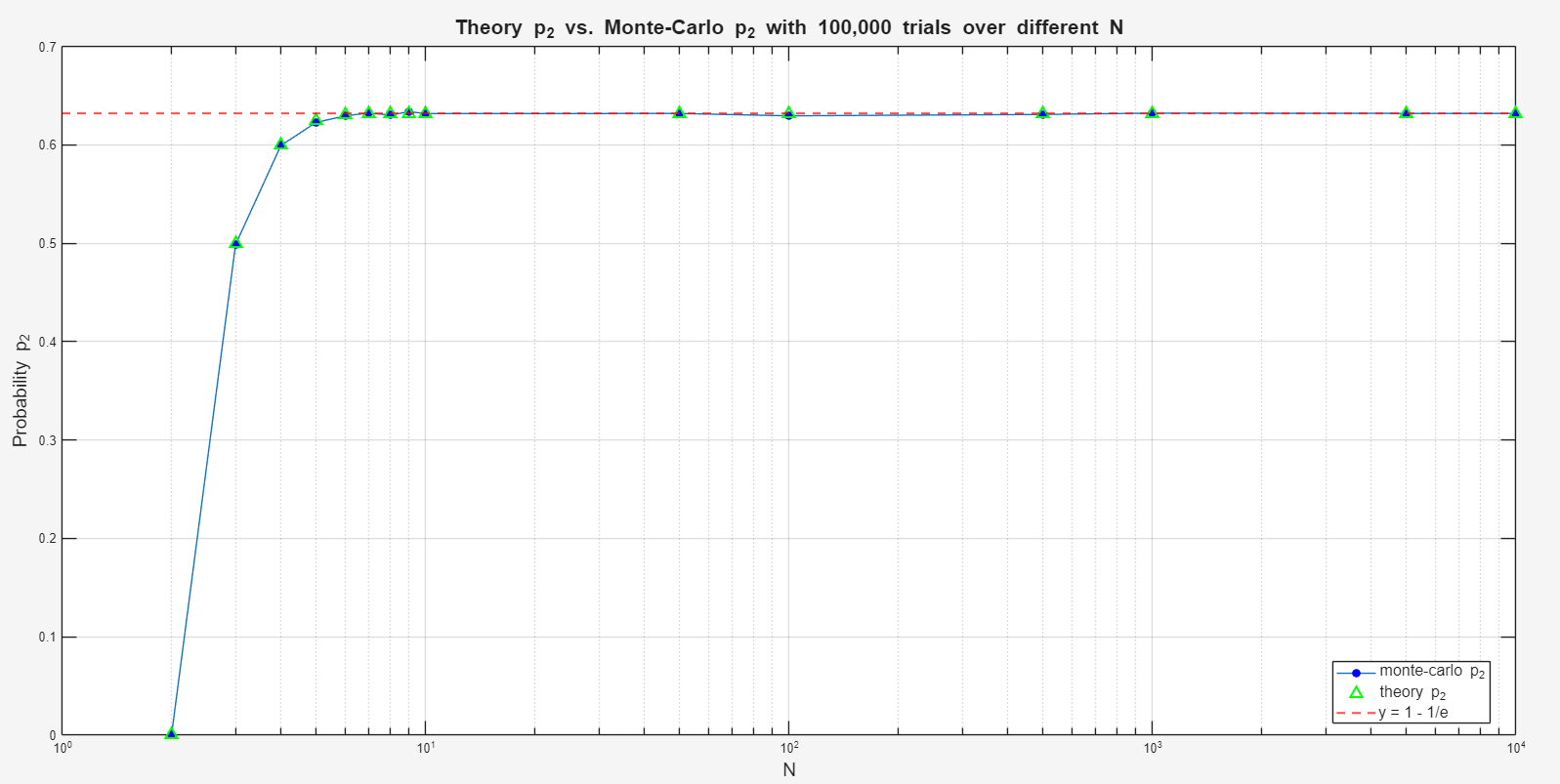
So, it looks like our friend frog is not just happy sitting on lily pad #1, but rather on a natural log base!