



March 21, 2025
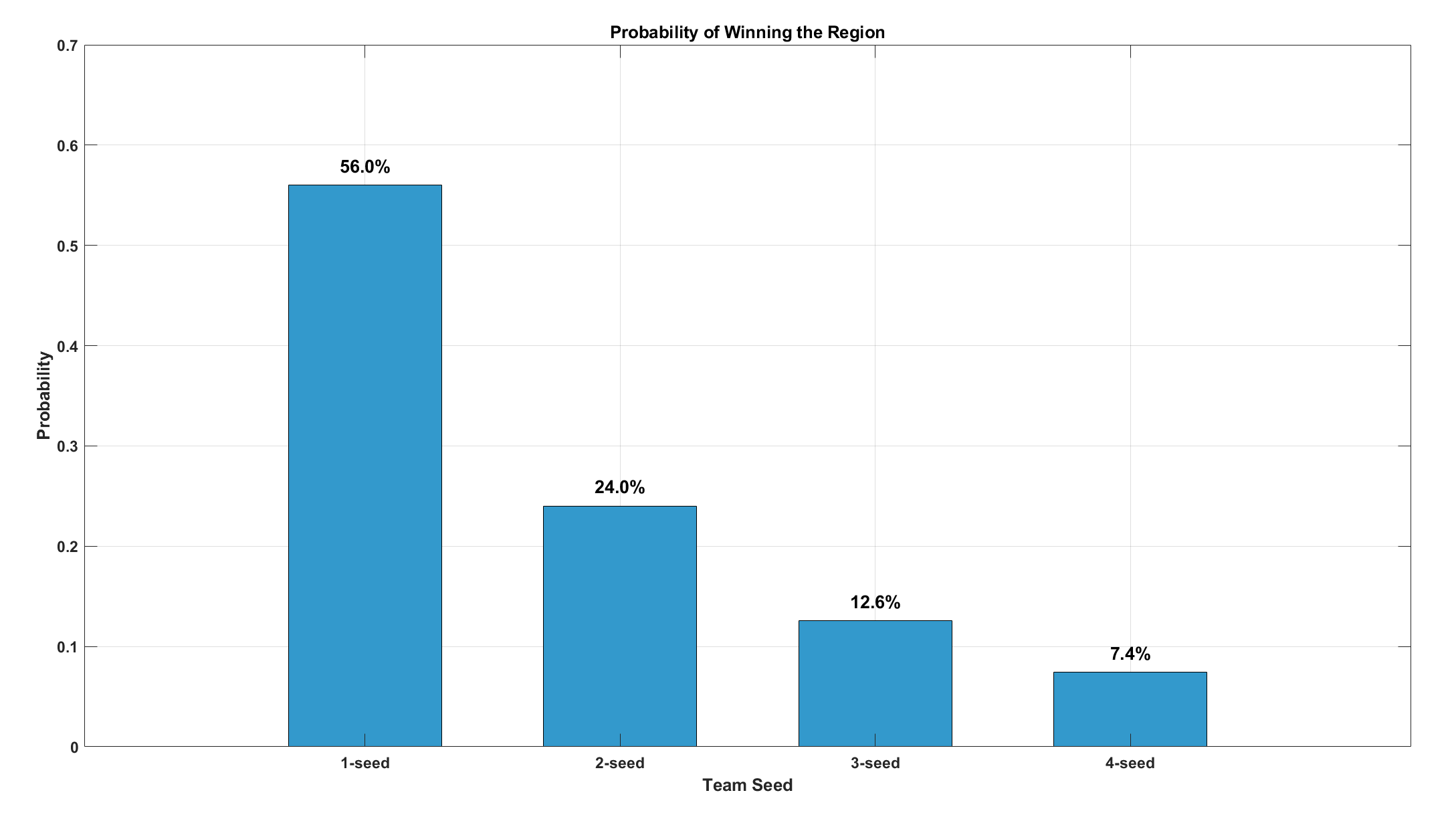
Fiddler answer: \(\frac{14}{25} = 56\%\)
Extra Credit: Approximately \(52\%\) as the number of rounds goes to infinity.
Explanation:
March Madness is upon college basketball fans, and we are going to celebrate via March Mathness. In the original puzzle, there are only four teams and they are seeded 1 through 4. In the semi-finals, 1 vs. 4 and 2 vs. 3 and the winners of the respective matchups move on to the Final. Given the probability that \(M\)-seed wins over \(N\)-seed with probability of \(\frac{N}{M+N}\) and vice-versa, we have the following calculations to see the probability that 1-seed wins.
\begin{align} &\text{Probability that 1-seed wins out} \\ \\ =& \text{ Probability that 1-seed wins over 4-seed} \\ &\times \text{ Probability that 1-seed wins over the winner of the 2-3 matchup} \\ \\ =& \frac{4}{5} \left(\frac{2}{3}\times\frac{3}{5} + \frac{3}{4}\times\frac{2}{5}\right) \\ \\ =& \frac{4}{5} \left(\frac{2}{5} + \frac{3}{10}\right) \\ \\ =& \frac{4}{5} \left(\frac{7}{10}\right) \\ \\ =& \boxed{\frac{14}{25}} = 56 \% \end{align}
We can use the same method to figure out the probability that the other teams win out, and ensure that the total sum to 1.
\begin{align} &\text{Probability that 2-seed wins out} \\ \\ =& \text{ Probability that 2-seed wins over 3-seed} \\ &\times \text{ Probability that 2-seed wins over the winner of the 1-4 matchup} \\ \\ =& \frac{3}{5} \left(\frac{1}{3}\times\frac{4}{5} + \frac{4}{6}\times\frac{1}{5}\right) \\ \\ =& \frac{3}{5} \left(\frac{4}{15} + \frac{2}{15}\right) \\ \\ =& \frac{3}{5} \left(\frac{6}{15}\right) \\ \\ =& \frac{6}{25} = 24 \% \end{align}
\begin{align} &\text{Probability that 3-seed wins out} \\ \\ =& \text{ Probability that 3-seed wins over 2-seed} \\ &\times \text{ Probability that 3-seed wins over the winner of the 1-4 matchup} \\ \\ =& \frac{2}{5} \left(\frac{1}{4}\times\frac{4}{5} + \frac{4}{7}\times\frac{1}{5}\right) \\ \\ =& \frac{2}{5} \left(\frac{1}{5} + \frac{4}{35}\right) \\ \\ =& \frac{2}{5} \left(\frac{11}{35}\right) \\ \\ =& \frac{22}{175} \approx 13 \% \end{align}
\begin{align} &\text{Probability that 4-seed wins out} \\ \\ =& \text{ Probability that 4-seed wins over 1-seed} \\ &\times \text{ Probability that 4-seed wins over the winner of the 2-3 matchup} \\ \\ =& \frac{1}{5} \left(\frac{2}{6}\times\frac{3}{5} + \frac{3}{7}\times\frac{2}{5}\right) \\ \\ =& \frac{1}{5} \left(\frac{1}{5} + \frac{6}{35}\right) \\ \\ =& \frac{1}{5} \left(\frac{13}{35}\right) \\ \\ =& \boxed{\frac{13}{175}} \approx 7 \% \end{align}
We can verify that all four probabilities total to one.
Below is a bar graph of the winning probabilities of each of the four teams:
For extra credit, I performed Monte-Carlo to simulate the probability of the 1-seed winning out given \(k\) rounds of \(2^k\) teams with the bracket rule laid out in the puzzle. Here I simulated until \(k = 12\), that is, with a 4096-player tournament (!) and got the following result:
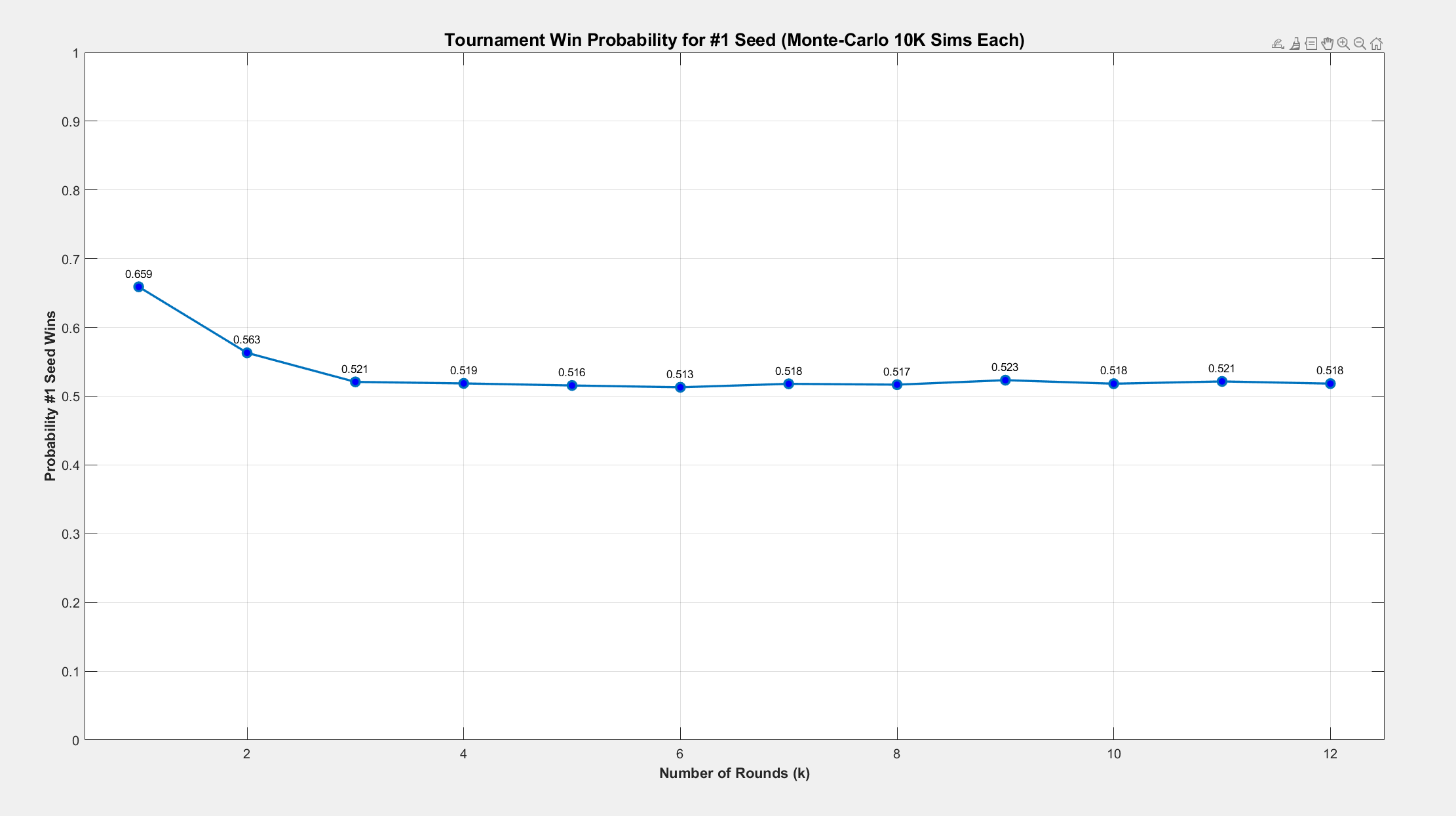
Simulation code is available upon request. From the chart, it appears that as \(k \to \infty\), the probability that the one-seed wins out stabilizes around 0.52, or 52%.