Fiddler on the Proof: Jun 14, 2024

David Ding

Jun 14, 2024

Can You Pack the Circles?

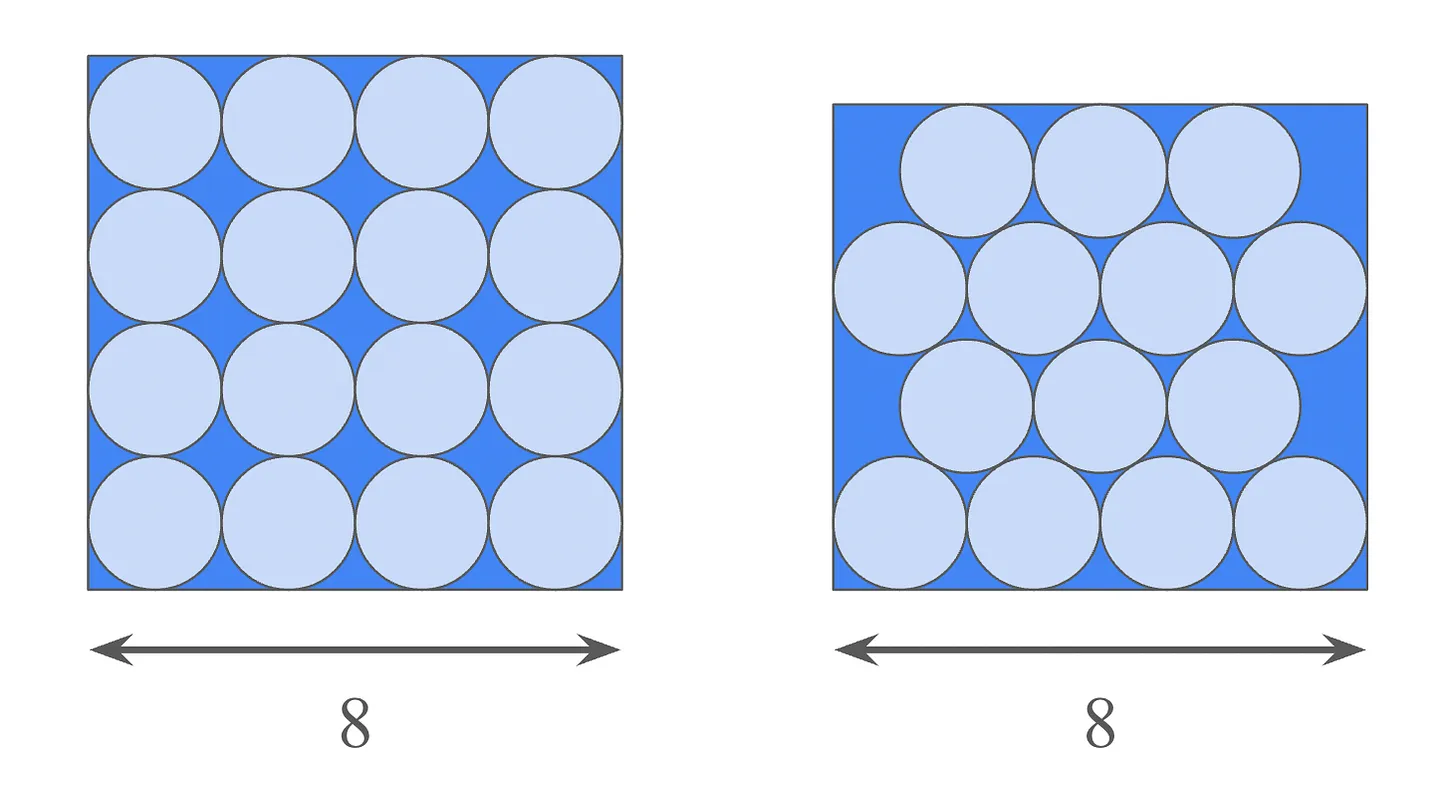
You want to pack four rows of unit circles into a rectangle with a base of 8. You’re considering two strategies for packing:

1. Square packing. In this case, four rows of circles each are packed in an array of squares.
2. Hexagonal packing. In this case, the bottom row has four circles, and higher rows alternate between having three and four circles.

The following diagram shows the square-packed and hexagonal-packed rectangles on the left and right, respectively:

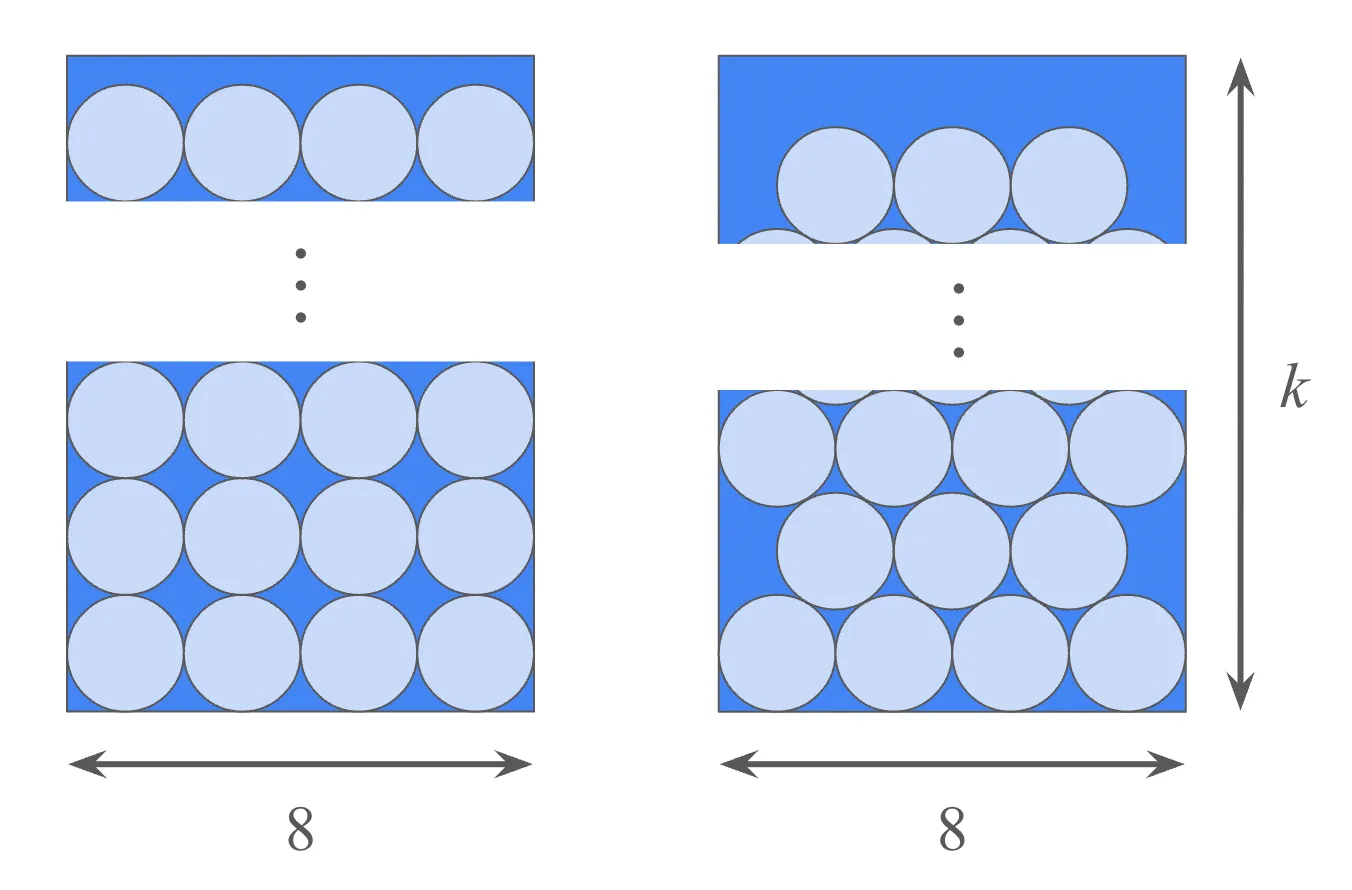
For extra credit, consider a large space of 8 x \(k\) rectangle. For what value of \(k\) will hexagonal packing start to always become strictly more efficient than square packing?

Explanation:

First, observe that for square packing, the packing efficiency is independent of number of rows, as each row is packed the same way as one another. Therefore, we can calculate the packing efficiency by looking at the per-row efficiency. We have:

\begin{align} &\text{Square Packing Efficiency} \\ \\ &= \frac{\text{Total Area of Circles}}{\text{Total Area of Rectangle}} \\ \\ &= \frac{4 \times \pi}{8 \times 2} \\ \\ &= \boxed{\frac{\pi}{4}}\\ \\ &\approx 78.5 \% \end{align}

Next, for the hexagonal packing case, we notice that regardless of whether the new row has three or four circles, the amount of height added to the fitting rectangle is always the same. So, let us first calculate the height added, which we can use the Pythagorean theorem as the diagram below illustrates:

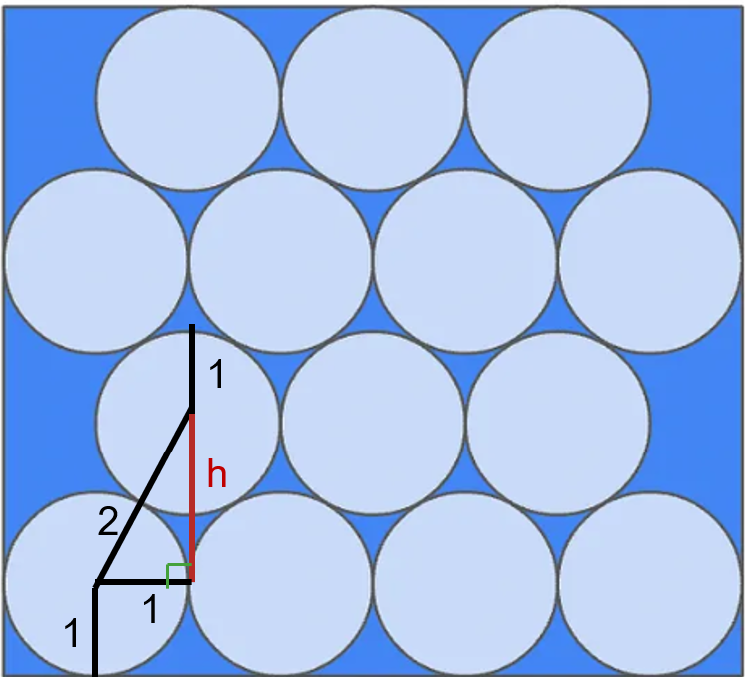
The old height is \(2\) (assuming we start with one row). The new height is \(1 + h + 1 = h + 2\). Therefore, the increase in height is \(h + 2 - 2 = h\) for each additional row we add. We can figure out \(h\) by using the Pythagorean Theorem of the right-angled triangle illustrated in the diagram above, which yields:

\begin{align} h &= \sqrt{2^2 - 1^2} \\ \\ &= \sqrt{4 - 1} \\ \\ &= \sqrt{3} \end{align}

Let's be ambitious here and figure out a function describing the hexagonal packing efficiency in terms of \(k\), the number of rows of circle we have. We are going to do this by looking at the fitting rectangle's area as well as the total area of circles, which are both going to be functions of \(k\) by themselves.

Starting with the rectangle's area. The initial height is \(2\) for \(k = 1\). Then, as \(k\) increments by 1, the total height increments by \(h = \sqrt{3}\) as calculated earlier. So, the function of the rectangle's area, call it \(r(k)\) for \(k = 1, 2, 3, \dots\) is:

\begin{align} r(k) &= 8(\sqrt{3} (k-1) + 2) \end{align}

Next, define \(c(k)\), the total area of circles as a function of \(k\) for \(k = 1, 2, 3, \dots\) The number of circles will increment either by three or four depending on the parity of \(k\). When \(k\) is odd, such as adding row 1, row 3, row 5, etc., we add four circles. On the other hand, when \(k\) is even, we add three circles. Therefore, the number of circles as a function of \(k\) is actually \(4\lceil{\frac{k}{2}}\rceil + 3\lfloor{\frac{k}{2}}\rfloor\). Since each circle is a unit circle, we have:

\begin{align} c(k) &= \pi \left(4\left\lceil{\frac{k}{2}}\right\rceil + 3\left\lfloor{\frac{k}{2}}\right\rfloor\right) \end{align}

Putting everything together, we have:

\begin{align} p(k) &= \text{Hexagonal Packing Efficiency} \\ \\ &= \frac{\text{Total Area of Circles}}{\text{Total Area of Rectangle}} \\ \\ &= \frac{c(k)}{r(k)} \\ &= \boxed{\frac{\pi \left(4\left\lceil{\frac{k}{2}}\right\rceil + 3\left\lfloor{\frac{k}{2}}\right\rfloor\right)}{8(\sqrt{3} (k-1) + 2)}}\\ \end{align}

For the original problem, \(k = 4\), and so we have:

\begin{align} p(4) &= \frac{c(4)}{r(4)} \\ &= \boxed{\frac{14 \pi}{8(3\sqrt{3} + 2)}}\\ \\ &\approx 76.4 \% \end{align}

Therefore, for \(k = 4\), square packing is more efficient.

For extra credit, I first used MATLAB to plot \(p(k)\) and compared it against the baseline, which is the constant square packing efficiency of 78.5%. Here is what I get:

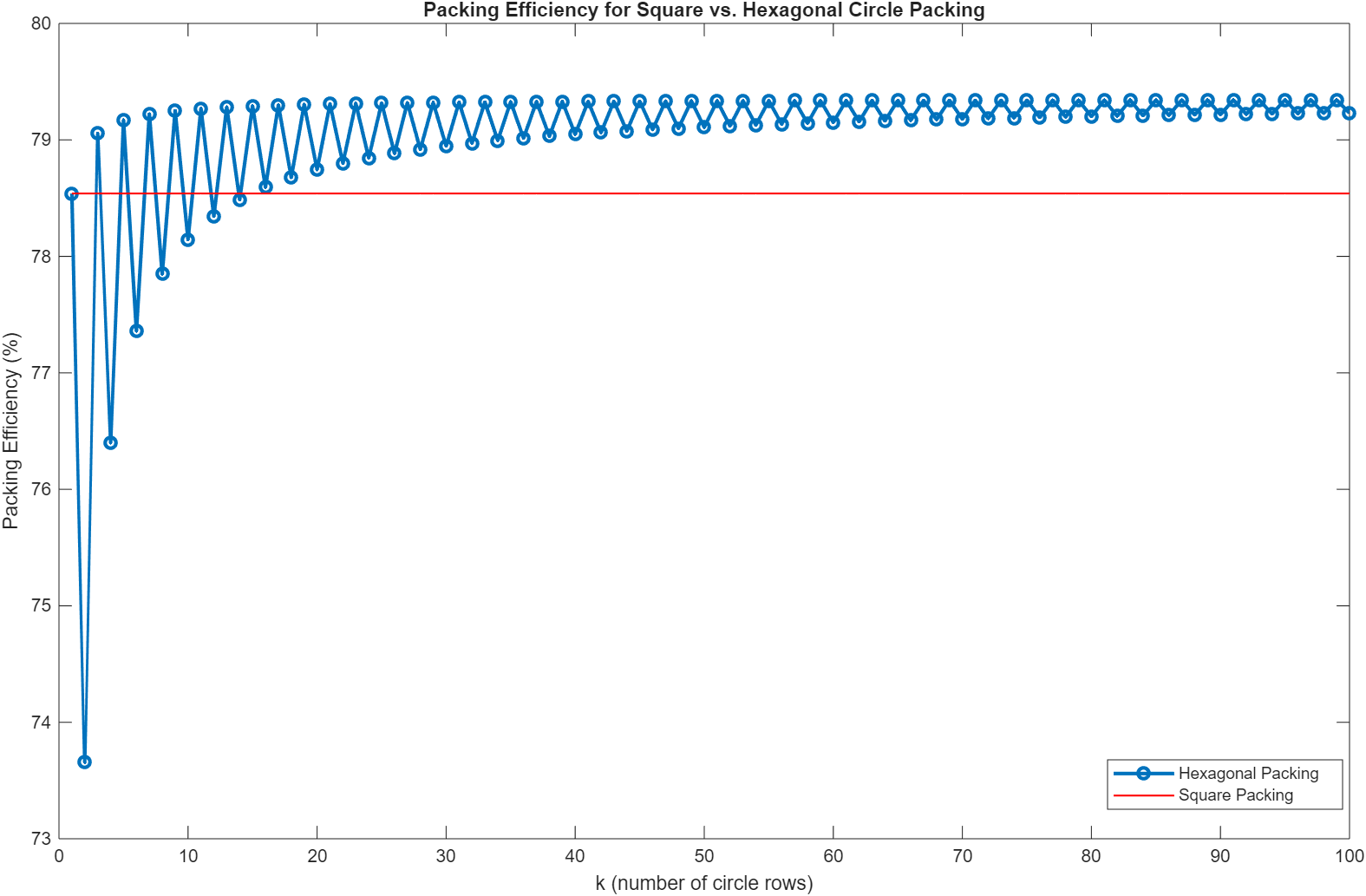
By inspection, the last time hexagonal packing dips below square packing in terms of efficiency is when \(k = 14\). Therefore, starting with \(k = 15\), hexagonal packing becomes strictly more efficienct than its square counterpart.

The last bit of proof to ensure that hexagonal packing never dips below square packing is to look at the limit of \(p(k)\) when \(k \to \infty\). Since we are dealing with ceiling and floor functions, we can use squeeze theorem by considering the upper bound where all terms of \(\left\lceil{\frac{k}{2}}\right\rceil\) and \(\left\lfloor{\frac{k}{2}}\right\rfloor\) become \(\frac{k + 1}{2}\), as well as the lower bound when those terms become \(\frac{k}{2}\). In both cases, the limit goes to \(\frac{7 \pi}{16 \sqrt{3}}\). The decreasing oscillating behavior is also observed in the graph above and is approaching that value. That is:

\begin{align} \lim_{k \to \infty} p(k) &= \frac{7 \pi}{16 \sqrt{3}} \\ \end{align}

This value is approximately 0.7935 or 79.4%. This is higher than the square packing efficiency of 78.5%. This means that in the limit, hexagonal circle packing will always be more efficient than square packing, and it is strictly more efficient starting with \(k = 15\).

Finally, as the Fiddler extra credit asked \(k\) to be the height of the rectangle for hexagonal packing, we just calculate that by making use of \(r(k)\):

\begin{align} k &= \frac{r(15)}{8} \\ \\ &= 14\sqrt{3} + 2 \\ \\ &\approx 26.25 \end{align}