



Jul 12, 2024
From Chris Payne comes a tennis-themed puzzle that’s just in time for Wimbledon:
Consider a three-set tennis match. To win the match, you must win at least two of the three sets. To win a set, you must win a certain number of games. To win a game, you must win a certain number of points. For those who are unfamiliar with tennis, I’ll go into a little more detail.
A game is won by the first player who scores four points. However, the winner must “win by two.” So if both players have three points, they keep going until one player has two more points than their opponent, at which point the player with more points wins the game.
A set is won by the first player to win six games within the set. However, if both players have exactly five games each, then they play exactly two more games. If one player wins both of them, that player wins the set. If each player wins one of these games, so that they now have six games apiece, they proceed to a tiebreak.
A tiebreak is essentially a game that goes to seven points rather than four. The first to seven points wins, and players must win by two.
Keeping all this in mind, what is the greatest percentage of points (including tiebreak points) a player could lose in a three-set match, while still winning the match itself?
\(\frac{106}{168} = 63.10\%\)
Explanation:
Let's start by getting the tricky bit out of the way, namely, the tiebreakers. Since in theory, each game can last indefinitely as one must win by two points to win the game, it is at first glance not clear what's the maximum percentage of points one can lose while still win in the end. To tackle this, let's split the points over the course of a match into "regular" points and "tiebreak" points. Let \(a\) be the total number of regular points you lose, and \(b\) be the total number of regular points played in the entire match. Furthermore, let \(x\) be the number of points you lose in the tiebreakers, where for now, let's set \(x\) to be any real number greater than or equal to 0. Here, by "tiebreak points", I meant the extra points played in a game and any extra points played in the tiebreak game, not the initial points played in the tiebreak game up to 7 points. By this definition, the total number of tiebreak points played must be equal to \(2x\), since for you to win the game with tiebreak points involved, for every tiebreak point you lose, you must win at least one tiebreak point back to maintain the eventual 2 point lead as the minimum you need to win a game. Therefore, the percentage of points you lose while still winning the match can be expressed as a function of \(x\), as follows:
\begin{align} f(x) &= \frac{a + x}{b + 2x} \\ \end{align}
Let's take the derivative of \(f(x)\) with respect to \(x\):
\begin{align} f'(x) &= \frac{b + 2x - 2(a + x)}{(b + 2x)^2} \\ \\ f'(x) &= \boxed{\frac{b - 2a}{(b + 2x)^2}} \\ \end{align}
One observation is that the derivative is negative when \(2a > b\), that is, when you lose more than half of your regular points. It is positive when \(b > 2a\) and the function \(f(x)\) asymptotically approach the limit \(\frac{1}{2}\) as \(x \to \infty\).
This means that when you lose more than half of the total points played without tiebreaks, any tiebreak points will decrease the percentage of points you lose while still winning the match.
Now we have a strategy to tackle the original problem: we first examine the ways in which we can win the match without tiebreak points, i.e. obtain the possible values for \(a\) and \(b\), and then detemine whether or not \(\frac{a}{b}\) is greater than \(\frac{1}{2}\). If so, we do not need to consider adding any tiebreak points because that will decrease the percentage of points we lose in a match. Finally, we pick the scenario in which we still win with the most percentage of total points lost, and that will be our answer.
Let's completely lose the first set, since we don't need to win it to win the match. There are 4 points per game and 6 games in total for us to lose, and so that's 24 points in total.
Now that we lost the first set, we must win the next two sets to win the match. There are three ways to win the set in the losingest fashion possible: 6-4, 7-5, and 7-6 (with the tiebreaker game win). In each of the first-to-4 games, the losingest scoreline is 4-2. Please note that the moment we get to a 3-3 score line, tiebreak points are needed. Now, let's examine each scenario:
For the 6-4 win, we obviously completely lose the four games with no points won, so that is 16 points lost. In each of the 6 games we win, with no tiebreaks, we lose 2 and win 4 points each, and so we lose 12 points and win 24 points in total in the games that we win. Overall, in such a set, we lose 28 points out of a total of \(28 + 24 = 52\) points.
For the 7-5 win, again we completely lose the five games with no points won, so that is 20 points lost. In each of the 7 games we win, with no tiebreaks, we lose 2 and win 4 points each, and so we lose 14 points and win 28 points in total in the games that we win. Overall, in such set, we lose 34 points out of a total of \(34 + 28 = 62\) points.
Finally, for the 7-6 win, in the first 12 games where we go 6-6, we lose 4 times 6 plus 2 times 6 equals 36 points, and win 4 times 6 equals 24 points. Then, in the tiebreak game, we win 7 and lose 5 for a total of 41 points lost and only 31 points won. Or putting it another way, we lose 41 out of a total of 72 points.
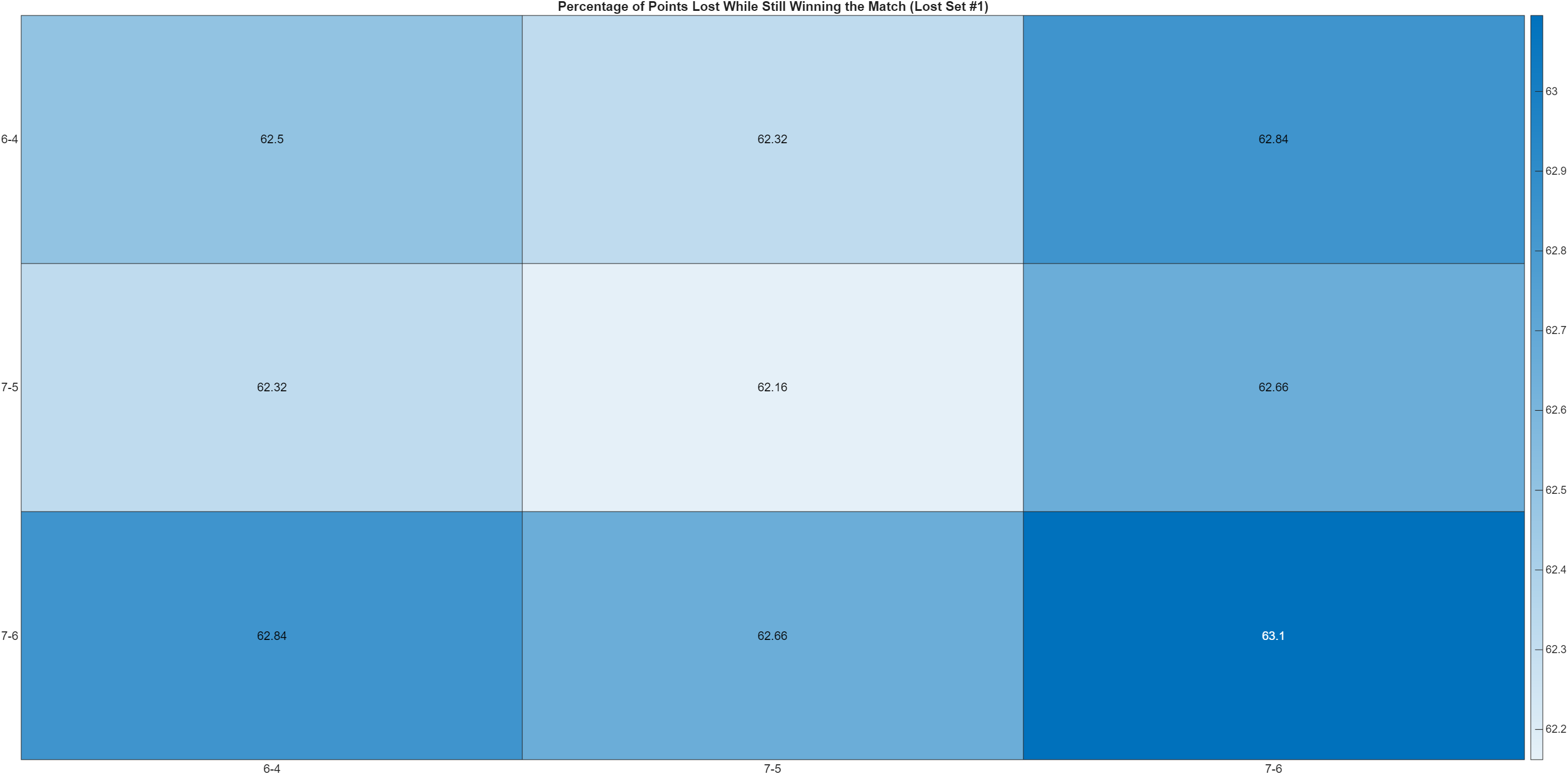
Finally, we put everything together by examining the various combinations of the above three scenarios applied to the last two sets, and also remembering to include the 24 points we lost in the first set. We have the following table of \(\frac{a}{b}\), where \(a\) is the total points we lose in the entire match out of a total of \(b\) points played in the match.
| Second Set/Third Set | 6-4 | 7-5 | 7-6 |
|---|---|---|---|
| 6-4 | \(\frac{80}{128} = 62.50\%\) | \(\frac{86}{138} = 62.32\%\) | \(\frac{93}{148} = 62.84\%\) |
| 7-5 | \(\frac{86}{138} = 62.32\%\) | \(\frac{92}{148} = 62.16\%\) | \(\frac{99}{158} = 62.66\%\) |
| 7-6 | \(\frac{93}{148} = 62.84\%\) | \(\frac{99}{158} = 62.66\%\) | \(\frac{106}{168} = 63.10\%\) |
Since all scenarios have the percentage greater than 50%, no extra tiebreak points are needed. As one can see, the combination that yields the greatest percentage of points lost is winning the remaining sets 7-6 apiece, with the tiebreak game won at 7-5, at 63.1%. The following heat chart illustrates the above table:
It is quite astonishing that you can lose more than 60% of your points in a tennis match and still win the whole thing!