Aug 16, 2024
Original Problem: \(\frac{a}{b} = \frac{2}{\pi - 2} \approx 1.75\)
Extra credit: \(\frac{a}{b}\) approaches \(2\) as \(\phi \to 0\)
Explanation:
Let us solve the general problem presented in the extra credit, as the original problem is just a special case of the general problem.
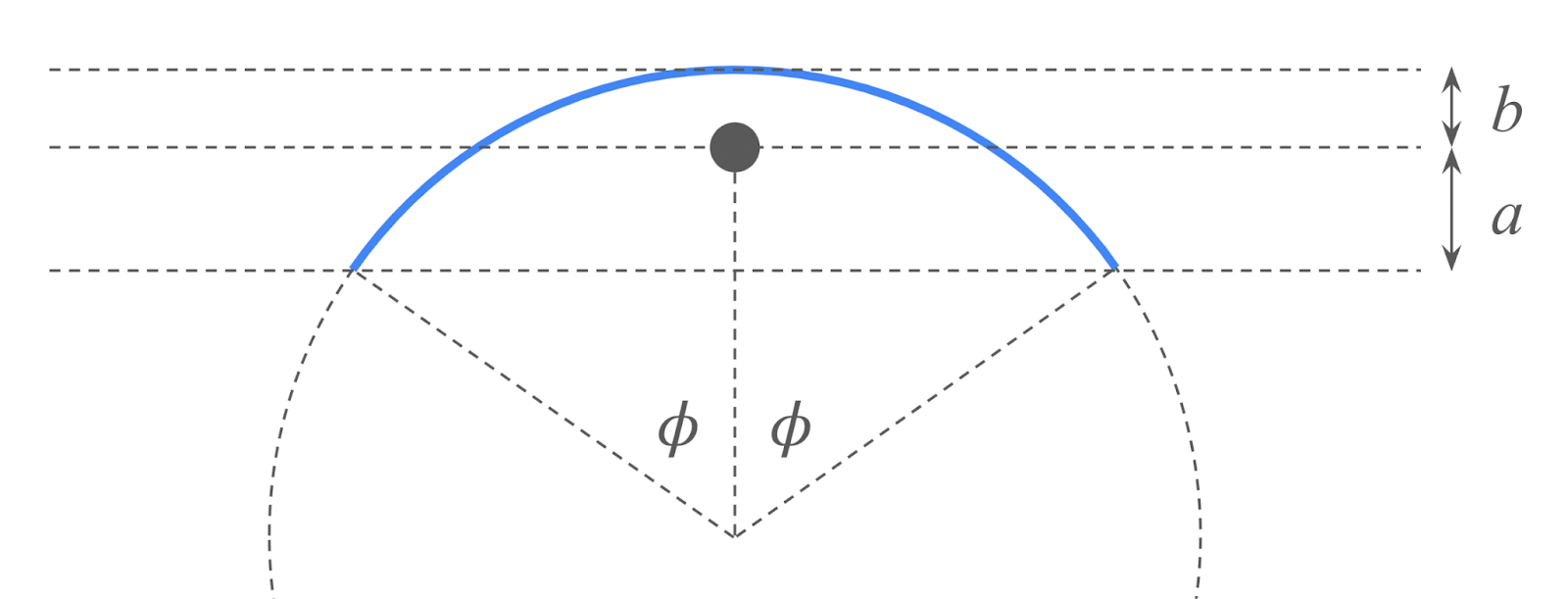
Technically, the problem is 2D, so for center of mass of an athelete's body modeled by an arc, there is the x-coordinate as well as the y-coordinate. Fortunately, by symmetry, the x-coordinate is right over the bar. It remains to find the y-coordinate. Note that when \(\phi = \frac{\pi}{2}\), the arc is a semi-circle.
Without loss of generality, let the semi-circle have a radius of 1. Furthermore, denote the distance between the bottom of the semi-circle (that is, when \(\phi = \frac{\pi}{2}\)) and the y-coordinate of the center of mass be \(h\). With this construction, we have:
\begin{align} a &= h - \cos{\phi} \\ b &= 1 - h \\ \end{align}
Where \(0 < \phi \leq \frac{\pi}{2}\).
We can find \(h\) using the definition of center of mass, as follows.
\begin{align} \int_{0}^{\phi} (\cos{\theta} - h) \,\mathrm{d}\theta &= 0 \\ \end{align}
In other words, the y-coordinate of the center of mass should yield zero when summed over the differences between it and the y-coordinates of all points on the arc, as we are assuming that the athlete's mass is evenly distributed. Solving for \(h\) in terms of \(\phi\), we get:
\begin{align} \int_{0}^{\phi} (\cos{\theta} - h) \,\mathrm{d}\theta &= 0 \\ \\ \sin{\theta} - h\theta |_{\theta = 0}^{\theta = \phi} &= 0 \\ \\ \sin{\phi} - h\phi &= 0 \\ \\ h &= \frac{\sin{\phi}}{\phi} \\ \end{align}
Thus we have:
\begin{align} a &= h - \cos{\phi} \\ \\ &= \frac{\sin{\phi}}{\phi} - \cos{\phi} \\ \\ &= \frac{\sin{\phi} - \phi \cos{\phi}}{\phi} \\ \\ b &= 1 - h \\ \\ &= 1 - \frac{\sin{\phi}}{\phi} \\ \\ &= \frac{\phi - \sin{\phi}}{\phi} \end{align}
Finally,
\begin{align} \frac{a}{b} &= \left(\frac{\sin{\phi} - \phi \cos{\phi}}{\phi}\right) \Biggm/ \left(\frac{\phi - \sin{\phi}}{\phi}\right) \\ \\ &= \boxed{\frac{\sin{\phi} - \phi \cos{\phi}}{\phi - \sin{\phi}}} \\ \end{align}
For the original problem, \(\phi = \frac{\pi}{2}\), and so plugging the value yields:
\begin{align} \frac{a}{b} &= \frac{\sin{\phi} - \phi \cos{\phi}}{\phi - \sin{\phi}} \\ \\ &= \frac{\sin{(\pi/2)} - (\pi/2) \cos{(\pi/2)}}{(\pi/2) - \sin{(\pi/2)}} \\ \\ &= \frac{1}{(\pi/2) - 1} \\ \\ &= \boxed{\frac{2}{\pi - 2}} \approx 1.75 \\ \end{align}
For the extra credit, we need to evaluate:
\begin{align} &\lim\limits_{\phi \to 0} \frac{\sin{\phi} - \phi \cos{\phi}}{\phi - \sin{\phi}} \\ \\ =& \lim\limits_{\phi \to 0} \frac{\cos{\phi} - (\cos{\phi} - \phi \sin{\phi})}{1 - \cos{\phi}} \quad \text{(L'Hôpital's rule)} \\ \\ =& \lim\limits_{\phi \to 0} \frac{\phi \sin{\phi}}{1 - \cos{\phi}} \\ \\ =& \lim\limits_{\phi \to 0} \frac{\sin{\phi} + \phi \cos{\phi}}{\sin{\phi}} \quad \text{(L'Hôpital's rule again)} \\ \\ =& \lim\limits_{\phi \to 0} \frac{\cos{\phi} + (\cos{\phi} + \phi \sin{\phi})}{\cos{\phi}} \quad \text{(L'Hôpital's rule one more time)} \\ \\ =& \frac{2}{1} = \boxed{2} \end{align}
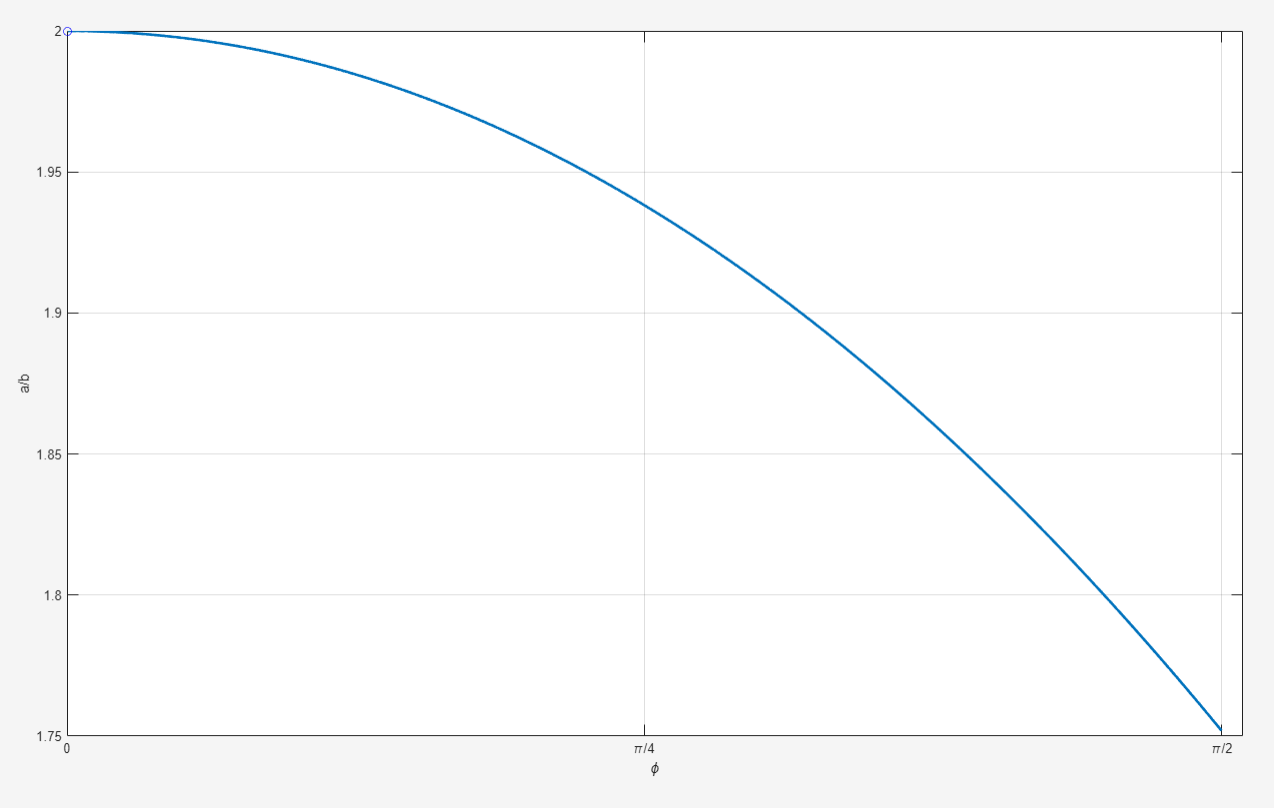
Below is a plot of the ratio \(\frac{a}{b}\) as a function of \(\phi\) for \(0 < \phi \leq \frac{\pi}{2}\).
