Fiddler on the Proof: Oct 11, 2024

David Ding

Oct 11, 2024

Will You Top the Leaderboard?

Explanation:

Here I used Monte-Carlo, which is a bit of a coding challenge to ensure that the simulation exactly matches the description of the puzzle. I used MATLAB and the codes are given at the end if you want to reproduce it yourself.

If at the halfway mark of 15 minutes, your rank is 0.5 (i.e. 50th percentile), then you can expect to be at 0.26 of the leaderboard, i.e. 74th percentile at the end of your ride after 30 minutes.

For completeness, I also simulated your final rank at other starting halfway ranks from 0 to 1 at 0.05 increments. I simulated via 1 million other riders at all times and averaged out over 10 iterations.

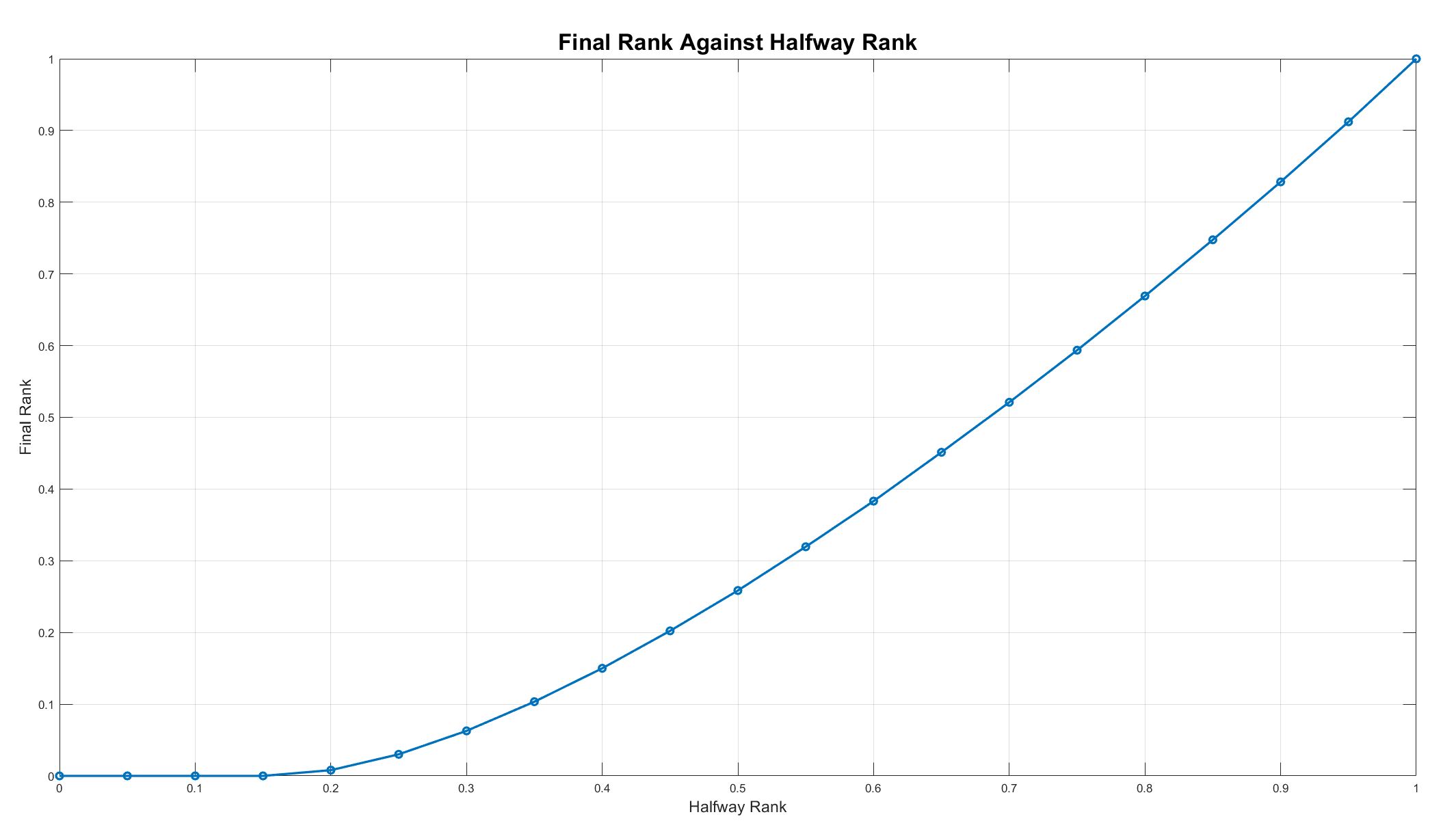
An interesting thing to note is that if you are in the 30th percentile at the halfway mark (i.e. 0.7 of the total rankings), you can expect to finish at the halfway rank. Another thing to notice is that you are almost guaranteed to top the leaderboard if you are within the top 15% of all riders at the halfway mark, as those that are ahead of you at that time are almost guaranteed to have ridden for more than 15 minutues, thereby dropping out of the leaderboard by the time you finish your ride.

Monte-Carlo simulation code via MATLAB:

function finalRank = getFinalRankMC(maxPower, maxTime, halfwayRank)
    % Get your final rank given max power of riders, max time, and your
    % halfway rank as a fraction between 0 and 1 (0-->leader; 1-->bottom
    % feeder).
    % time is in seconds
    % energy is in KiloJoules
    % power is in Watts

    % One million other riders at all times.
    % You are inserted at the halfway rank after max time/2.
    % your energy is uniformly distributed between the two riders in which
    % you are inserted, and everyone's powers are assumed constant.
    % you ride until max time.
    % new riders are inserted based on how many riders are removed at max
    % time.

    NUM_RIDERS = 1e6;
    ridersPowers = maxPower * rand(NUM_RIDERS, 1);
    ridersTimes = maxTime * rand(NUM_RIDERS, 1);
    ridersEnergy = ridersPowers .* ridersTimes / 1000; % convert to KJ
    unsortedRidersRanks = [ridersEnergy, ridersTimes];

    ridersRanks = sortrows(unsortedRidersRanks, 'descend'); % Assume more energy = higher rank

    % Inserting you as a rider at the halfway rank
    lowRiderRank = max(1, floor(NUM_RIDERS * halfwayRank));
    highRiderRank = min(lowRiderRank + 1, NUM_RIDERS);
    lowEnergy = ridersRanks(lowRiderRank, 1);
    highEnergy = ridersRanks(highRiderRank, 1);
    yourEnergyHalfway = (highEnergy - lowEnergy) * rand() + lowEnergy;

    % Next get the remaining riders
    remainingRidersRanks = ridersRanks(ridersRanks(:, 2) <= maxTime/2, :);
    [numRemainingRiders, ~] = size(remainingRidersRanks);

    numNewRiders = NUM_RIDERS - numRemainingRiders;
    newRidersPowers = maxPower * rand(numNewRiders, 1);
    newRidersTimes = (maxTime/2) * rand(numNewRiders, 1);
    newRidersRanksUnsorted = newRidersPowers.*newRidersTimes / 1000;

    % Now we need to update the existing riders rankings if they have not
    % exited the leaderboards after max time by how much more energy they
    % contribute in max time - (max time / 2) = max time / 2
    existingRidersUpdatedEnergy = remainingRidersRanks(:, 1) + ...
        (remainingRidersRanks(:, 1) ./ (remainingRidersRanks(:, 2))) * (maxTime/2);

    % Update your energy as well
    yourEnergy = yourEnergyHalfway * 2;

    % Get final rankings
    finalRankingsUnsorted = [newRidersRanksUnsorted; existingRidersUpdatedEnergy; yourEnergy];
    finalRankingsSorted = sort(finalRankingsUnsorted, 'descend');
    
    % Retrieve your rank
    [~, finalRank] = ismember(yourEnergy, finalRankingsSorted);

    finalRank = finalRank / (NUM_RIDERS + 1);
end
	

Simulation script:

%% Main script
NUM_ITER = 10;

maxPower = 200;
maxTime = 1800;
halfwayRankVec = linspace(0, 1, 21);
finalRankVec = zeros(1, length(halfwayRankVec));

for k = 1:length(halfwayRankVec)
    halfwayRank = halfwayRankVec(k);
    fprintf('Sim for halfwayRank %.2f\n', halfwayRank);
    sumRank = 0;
    for n = 1:NUM_ITER
        sumRank = sumRank + getFinalRankMC(maxPower, maxTime, halfwayRank);
    end
    finalRankVec(k) = sumRank / NUM_ITER;
end

%% Plot
figure;
plot(halfwayRankVec, finalRankVec, '-o', 'LineWidth', 2);
grid on;
title('Final Rank Against Halfway Rank', 'FontSize', 20);
xlabel('Halfway Rank', 'FontSize', 14);
ylabel('Final Rank', 'FontSize', 14);

%% Save data
save('mcData.mat', 'halfwayRankVec', 'finalRankVec');