



Oct 18, 2024
Radius is \(\sqrt{\frac{2}{3}}\) of a foot.
Extra Credit: Radius is \(\frac{2\sqrt{5}}{5}\) of a foot.
Explanation:
For the hemisphere bowl, let \(h\) denote the height of the cylindrical bore hole and let \(r\) denote the radius of the bore hole. Clearly, \(0 < h < 1\). In order to find the optimal \(h\), and hence the optimal \(r\) that maximizes the volume of the bore hole, I created the following diagram of the sideview of the bread bowl (igloo):

Where the highlighted area is where the bore hole is created. The key observation is that the side view of the whole setup yields a right-angled triangle with hypotenuse equal to the radius of the hemisphere, which is given to be 1 ft. Therefore, we can see that \(r^2 = (1 - h^2)\). Plugging this value to the volume of the cylinder, which is \(\pi r^2 h\), we get the volume as a function of \(h\):
\begin{align} f(h) &= \pi (1 - h^2)h \end{align}
For which \(0 < h < 1\). We can then find the critical points of \(f(h)\) to look at the optimal values for \(h\).
\begin{align} f(h) &= \pi (1 - h^2)h \\ \\ &= \pi (h - h^3) \\ \\ f'(h) &= \pi (1 - 3h^2) = 0 \\ \\ h^* &= \sqrt{\frac{1}{3}} \\ \\ \end{align}
We only take the positive solution as \(0 < h < 1\), and we note that \(h^* = \sqrt{\frac{1}{3}}\) is indeed between 0 and 1. We note that \(f''(h^*) < 0\) which means the function is concave down at that critical point of \(h\), meaning at \(h = h^*\), we have the maximum point for \(f(h)\). This means that:
\begin{align} r^* &= \sqrt{(1 - (h^*)^2)} \\ \\ r^* &= \sqrt{1 - \frac{1}{3}} \\ \\ r^* &= \boxed{\sqrt{\frac{2}{3}}} \end{align}
And the maximum volume we get is:
\begin{align} f(h^*) &= \frac{2\pi}{3} \sqrt{\frac{1}{3}} \\ \\ &= \frac{2\sqrt{3}\pi}{9} \\ \end{align}
For extra credit, we have a spherical bowl to begin and we can use the curved bottom of the bowl as part of the bore hole. This is illustrated in the following diagram I created:
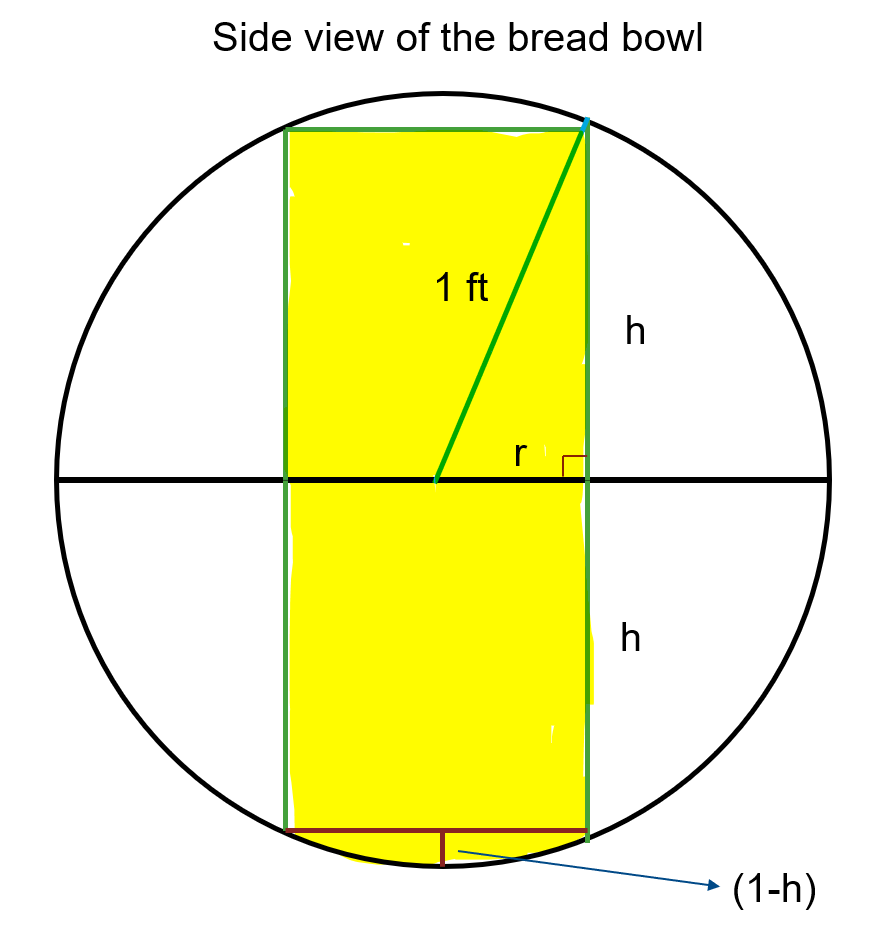
Once again the highlighted area is where the bore hole is created. Here we must make use of the spherical cap formula to calculate the extra portion below the cylindrical volume of the bore hole, which has a cap height of \((1 - h)\). Once again, we express the volume as a function of \(h\), where \(h\) is denoted in the diagram above.
\begin{align} f(h) &= \pi (1 - h^2)(2h) + \pi (1 - h)^2 - \pi\frac{(1 - h)^3}{3} \\ \\ &= \frac{\pi}{3} (-5h^3 + 3h + 2) \\ \\ f'(h) &= \frac{\pi}{3} (-15h^2 + 3) = 0 \\ \\ h^* &= \sqrt{\frac{1}{5}} \\ \\ \end{align}
Again, we only take the positive solution as \(0 < h < 1\), and we note that \(h^* = \sqrt{\frac{1}{5}}\) is indeed between 0 and 1. We again note that \(f''(h^*) < 0\) which means the function is concave down at that critical point of \(h\), meaning at \(h = h^*\), we have the maximum point for \(f(h)\). We can obtain \(r^*\) as follows:
\begin{align} r^* &= \sqrt{(1 - (h^*)^2)} \\ \\ r^* &= \sqrt{1 - \frac{1}{5}} \\ \\ r^* &= \boxed{\frac{2\sqrt{5}}{5}} \end{align}
And the maximum volume we get is:
\begin{align} f(h^*) &= \frac{\pi}{3} (-5h^3 + 3h + 2) |_{h = \sqrt{\frac{1}{5}}} \\ \\ &= \frac{2}{15} (5 + \sqrt{5}) \pi \\ \end{align}