Nov 8, 2024
\(p = \frac{1640}{2187} \approx 0.7499\)
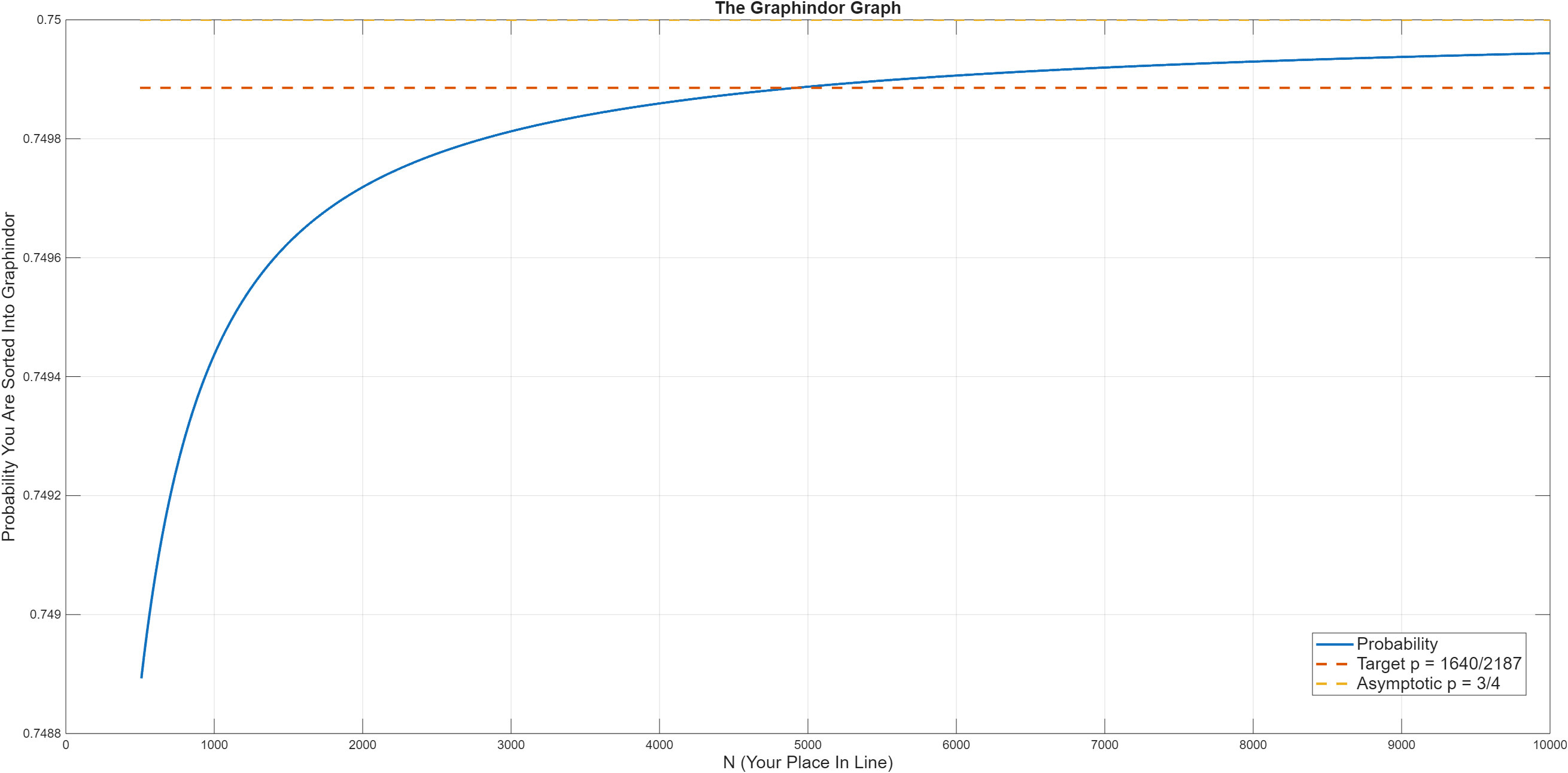
Extra Credit: \(N = 4922\)
Explanation:
Working backwards--this is the key to solving the original puzzle. Let \(p_k\) be the probability that the \(k\) th math wizard-to-be is to be sorted into Graphindor. Clearly, we want \(p_{10}\). Since the Sorting Hat grants your wish as long as the previous person did not get sorted into Graphindor, your probability only depends on the previous person's probability of getting sorted into Graphindor. That is, \(p_{10} = 1 - p_9\).
Now let's look at \(p_9\). Since one assumes others are equally likely to be sorted into any of the four houses, or any of the three if the requested house is forbidden, the probability that the ninth person is sorted into Graphindor would be \(\frac{1 - p_8}{3}\). This continues backwards until \(p_3\). From the givens in the puzzle, \(p_2 = 0\) and \(p_1 = 1\).
Thus, we have the following chart:
| \(k\) | \(p_k\) |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | \(\frac{1 - p_2}{3} = \frac{1}{3}\) |
| 4 | \(\frac{1 - p_3}{3} = \frac{2}{9}\) |
| 5 | \(\frac{1 - p_4}{3} = \frac{7}{27}\) |
| 6 | \(\frac{1 - p_5}{3} = \frac{20}{81}\) |
| 7 | \(\frac{1 - p_6}{3} = \frac{61}{243}\) |
| 8 | \(\frac{1 - p_7}{3} = \frac{182}{729}\) |
| 9 | \(\frac{1 - p_8}{3} = \frac{547}{2187}\) |
| 10 | \(1 - p_9 = \frac{1640}{2187}\) |
So the answer is \(p = p_{10} = \frac{1640}{2187} \approx 0.7499\), very close to \(\frac{3}{4}\) as one would intuitively think. This is because in general, there is a one in four chance that the person in front of you gets sorted into Graphindor, in which you would not be sorted into your desired house. In all other scenarios, you would be a Grapindor student!
Please note that in the limit, as \(N \to \infty\), the probability that you will be sorted into Graphindor, assuming you plan to request it to the Sorting Hat, approaches \(\frac{3}{4}\). This is because the person in front of you has a limiting probability of \(\frac{1}{4}\) of being sorted into Graphindor, as equally likely as being sorted into any of the four houses. For \(N = 10\) in the original puzzle, \(p = \frac{1640}{2187}\). The difference is \(\frac{3}{4} - \frac{1640}{2187} = \frac{1}{8748}\), an extremely small amount. Nonetheless, it's not quite 75%, so there is room for improvement.
Please note that the way we calculate \(N\) is the same as that for the original puzzle. So, I used computer to help me find that \(N\), courtesy of binary search. The code is below and it has three parts: two helper functions and the main script. All codes written in MATLAB.
function [prob, probVec] = getProb(M, N)
% Gets the probability that you are sorted into Graphindor given that
% the Mth student is sorted into Graphindor and you are Nth in line,
% where N > M
if N <= M
error('N must be greater than M!');
end
sizeOfVec = N - M;
probVec = NaN(sizeOfVec, 1);
probVec(1) = 0; % Since Mth student is already sorted into Graphindor.
if sizeOfVec == 1
prob = probVec(1);
return;
end
for k = 2:sizeOfVec-1
probVec(k) = (1 - probVec(k - 1))/3;
end
probVec(sizeOfVec) = 1 - probVec(sizeOfVec - 1);
prob = probVec(sizeOfVec);
end
***
function avgProb = getProbAvg(N)
% Given that you are Nth in line, get the average probability that you
% are sorted into Graphindor given that the Mth person is sorted into
% Graphindor, 1 <= M < N
probSum = 0;
for M = 1:N-1
probSum = probSum + getProb(M, N);
end
avgProb = probSum/(N - 1);
end
***
%% Main script to find N
target = 1640/2187;
N_low = 10;
N_high = 10000; % This value exceeds the target
N_mid = floor((N_low + N_high)/2);
ph = getProbAvg(N_mid);
pl = getProbAvg(N_mid - 1);
while ~(ph > target && pl <= target)
if ph <= target
N_low = N_mid;
N_mid = floor((N_low + N_high)/2);
else
N_high = N_mid;
N_mid = floor((N_low + N_high)/2);
end
ph = getProbAvg(N_mid);
pl = getProbAvg(N_mid - 1);
end
In the end, \(N = 4922\). The average probability that you are sorted into Graphindor is 0.749885693964641. This is marginally greater than \(p = \frac{1640}{2187} \approx 0.749885688157293\). If you were instead \(N - 1 = 4921\) in line, your probability drops to 0.749885670731707, which is marginally lower than the target \(p\).
Below is a graph showing everything we've talked about so far:
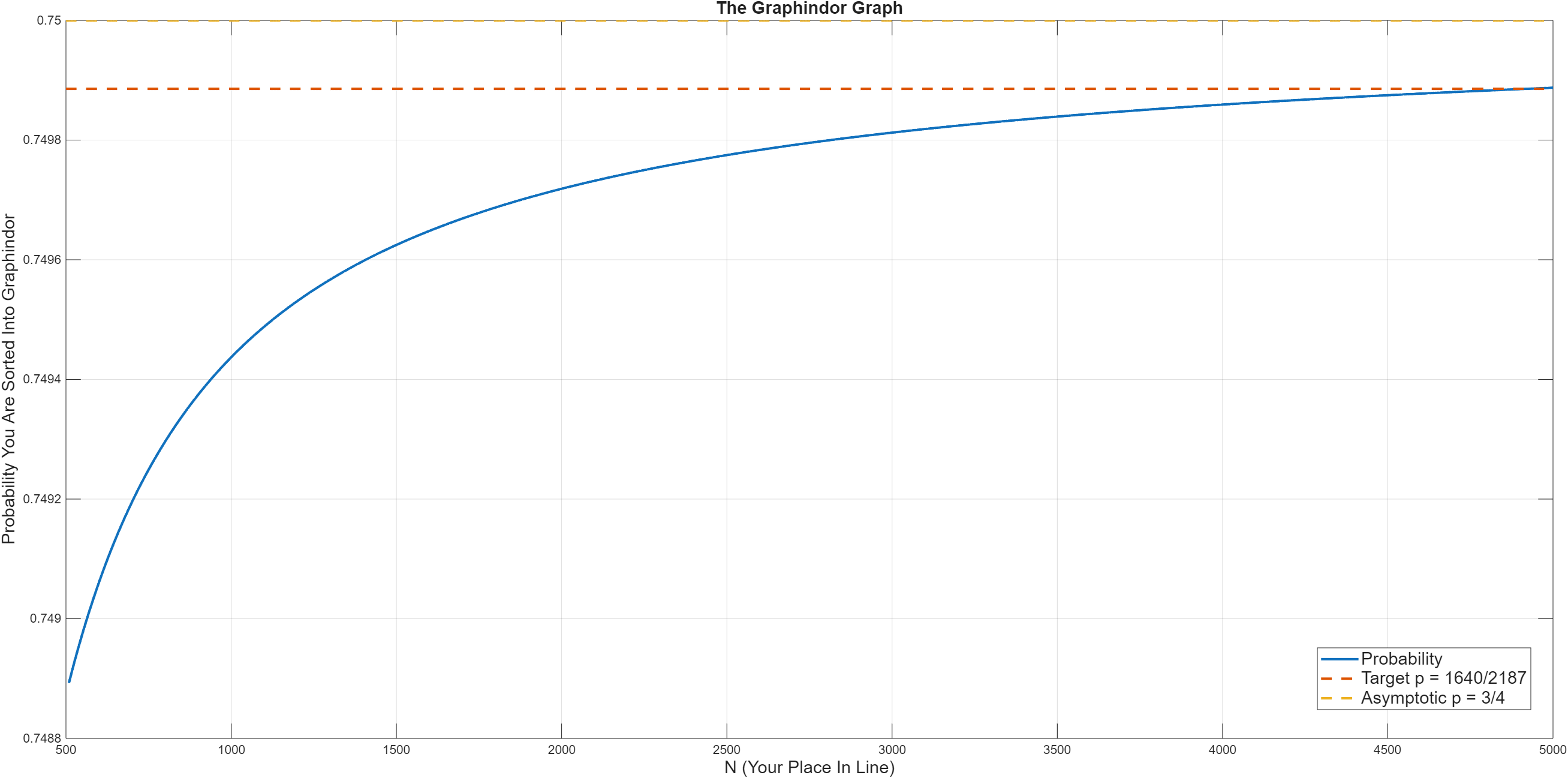
Here is the graph extended to \(N = 10000\):