



Dec 6, 2024
For \(N = 3\), min energy is 2.7071
Extra Credit: For \(N = 9\), min energy is 49.7587
Explanation:
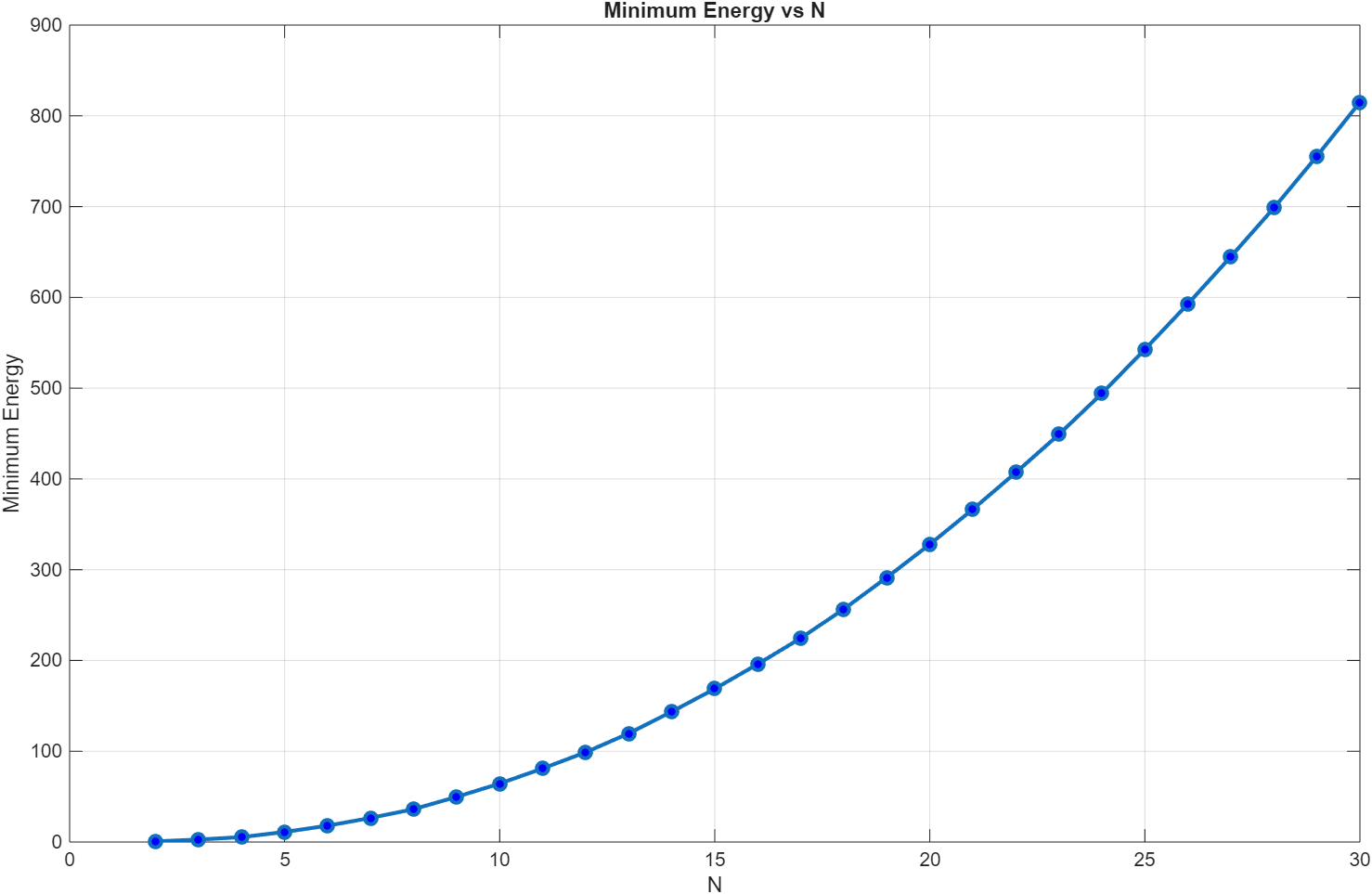
Assuming \(r\) is the Euclidean distance between two points, we have an optimization problem where we minimize the sum of each pairwise energy defined by the distance between the associated two points. Mapping the unit square onto a Cartesian plane where the lower left corner is at the origin, we have the lower bound constraints for each of the point co-ordinates at zero and upper bound at 1. I fed the optimization problem into "fmincon" function in MATLAB, and I got out the following for number of points, \(N\), going from 2 to 30:
dataSet =
30×2 cell array
{ 0×0 double} {0×0 double}
{ 4×1 double} {[ 0.7071]}
{ 6×1 double} {[ 2.7071]}
{ 8×1 double} {[ 5.4142]}
{10×1 double} {[ 11.0711]}
{12×1 double} {[ 17.9919]}
{14×1 double} {[ 26.5488]}
{16×1 double} {[ 36.2265]}
{18×1 double} {[ 49.7587]}
{20×1 double} {[ 64.4061]}
{22×1 double} {[ 81.0760]}
{24×1 double} {[ 98.8916]}
{26×1 double} {[119.6423]}
{28×1 double} {[143.5671]}
{30×1 double} {[168.7901]}
{32×1 double} {[196.0359]}
{34×1 double} {[224.6021]}
{36×1 double} {[256.6181]}
{38×1 double} {[291.4471]}
{40×1 double} {[327.9846]}
{42×1 double} {[366.5805]}
{44×1 double} {[407.0539]}
{46×1 double} {[448.9880]}
{48×1 double} {[494.1505]}
{50×1 double} {[542.7418]}
{52×1 double} {[592.7926]}
{54×1 double} {[644.9338]}
{56×1 double} {[698.5472]}
{58×1 double} {[755.6260]}
{60×1 double} {[815.0777]}
So, for \(N = 2\), the minimum energy is 0.7071. For \(N = 9\), the minimum energy is 49.7587.
Below is an animation on how the optimal packing patterns change with respect to \(N\):
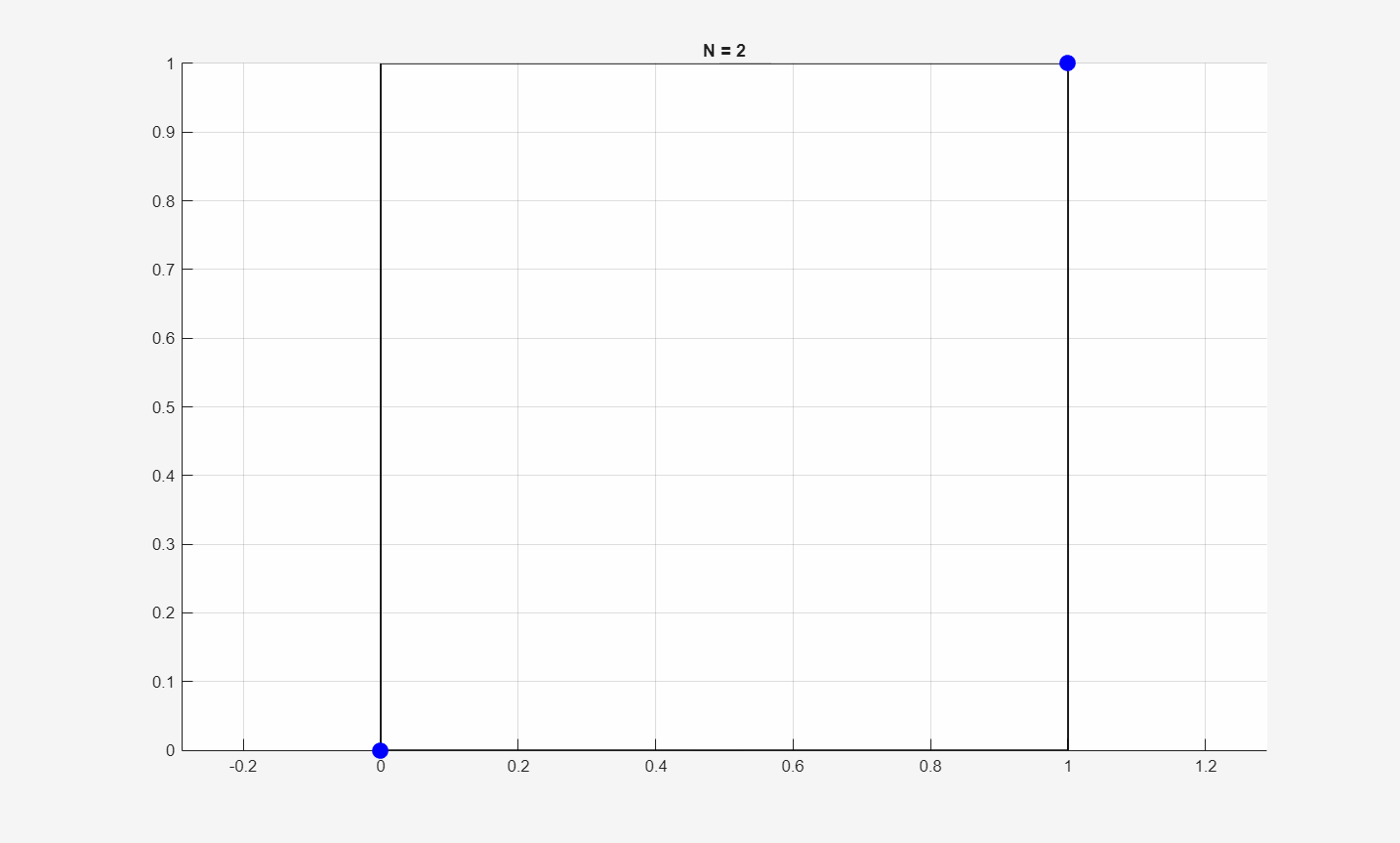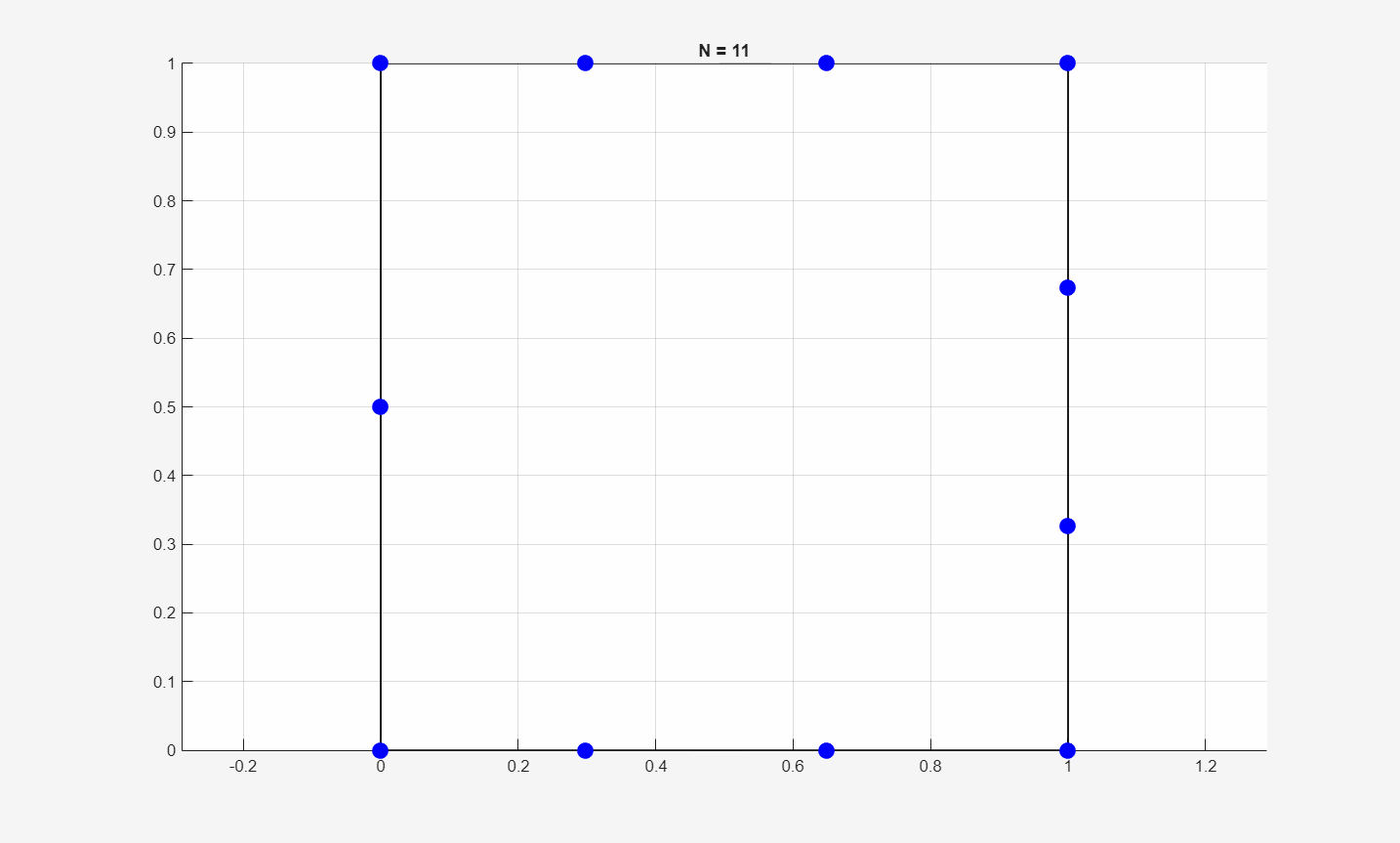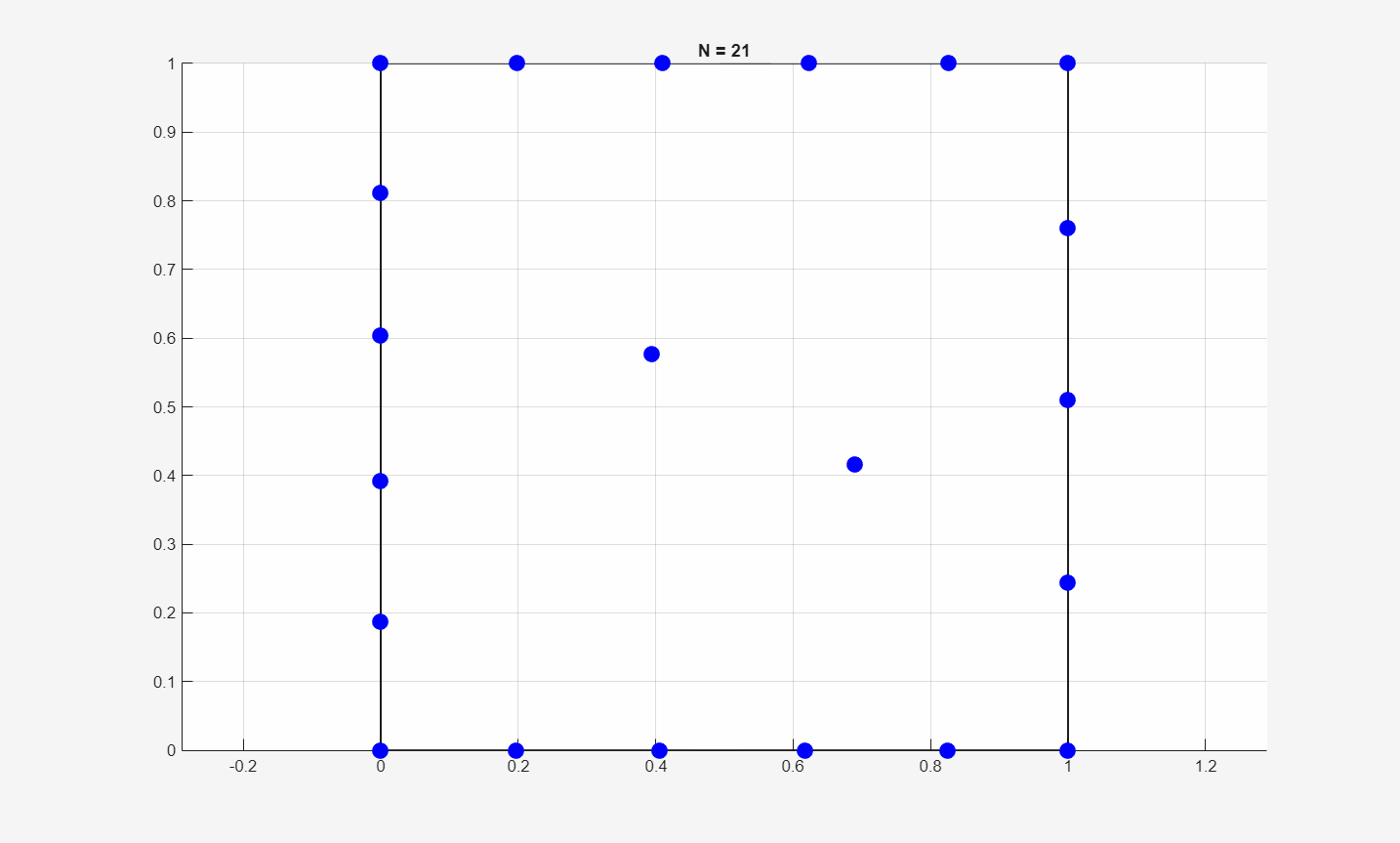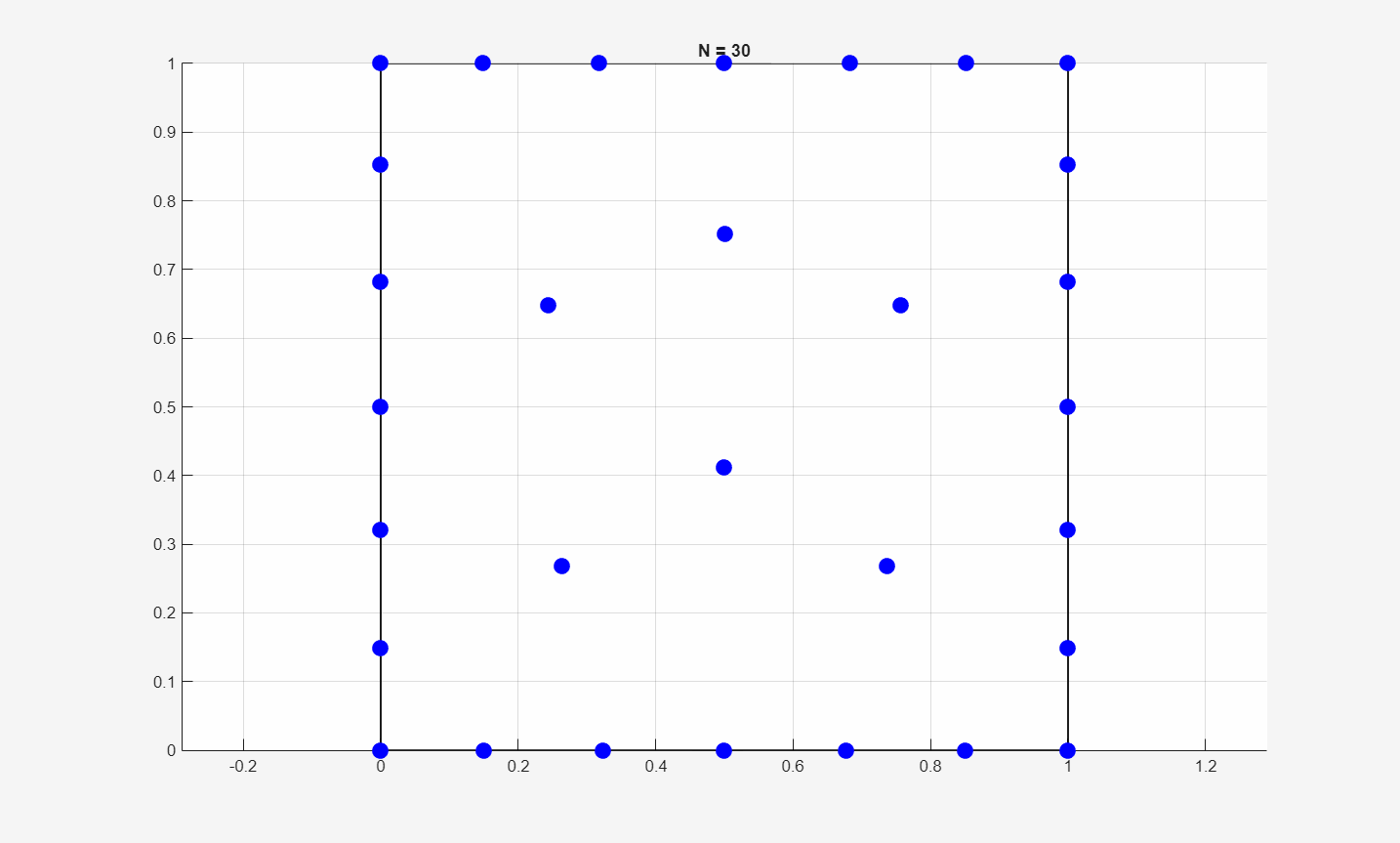
Below is the plot of the minimum energy values vs. \(N\):
I set the max interation to 10,000 for each solve and I performed 20 solves for each \(N\) where in each solve I started out with random points to increase the chance that a local minimum is the global minimum.