



December 13, 2020
"DAY 13 – How far apart are the centres of these two circles with radius 1, if all three shaded regions have the same area? (Careful, this one is difficult!) #math #puzzle"

Answer: \(d \approx 0.8079\)
Solution:
Mathigon is an online math education company that creates insightful textbooks geared towards inspiring the next generation of critical thinkers and problem solvers. Starting in December of this year they once again started their annual Mathigon Puzzle Calendar. Day 13 in particular intrigued me, not the least of the reasons being the first three-star puzzle in the calendar, but once I started solving it, I also realized several fields of mathematics are all involved in arriving the solution, which I found to be pretty neat. As a spoiler, the tools that I used, in order, are as follows:
Once again, this serves as a poignant reminder on how math is really well-connected.
Let \(d\) be the distance between the centers of the two circles. The first step is to use set arithmetic to actual figure out what is the common area shared by the three pieces of the overlapping circles. Treating each of the two circles as a set, and letting the shaded area have area of \(S\). The union of the two circles must have area \(3S\). The union is calculated by adding up the areas of the two circles, which are \(\pi\) each, then subtracting the double-counted bit, i.e. the shaded area in the middle. In the end we have: \begin{align} \pi + \pi - S &= 3S \\ 2\pi - S &= 3S \\ 4S &= 2\pi \\ S &= \frac{\pi}{2} \end{align} Therefore, all three shaded regions have area \(\frac{\pi}{2}\).
Next, I used analytic geometry to obtain the relevant parameters needed to calculate the distance \(d\). Analytic geometry is all about mapping the geometry shapes onto a coordinates plane, and using coordinates, slopes, equations of curves, etc. to help derive geometry values and properties. Therefore, without loss of generality (WLOG), let one of the circles be centered at the origin (0, 0). It will be a circle with equation: \begin{equation} x^2 + y^2 = 1 \end{equation}
Since the other circle is \(d\) apart from the first vis-a-vis the center, we will, WLOG, let it be positive \(d\) units to the right, along the x-axis, of the first circle (no shift in y). Therefore, it will have equation: \begin{equation} (x-d)^2 + y^2 = 1 \end{equation}
I can calculate the points of intersection for the two circles given the value of \(d\), as follows. Subtract the second equation from the first, we obtain: \begin{align} x^2 - (x-d)^2 &= 0 \\ [x - (x - d)][x + (x - d)] &= 0 \\ d(2x - d) &= 0 \\ \end{align} Either \(d\) is 0 or \((2x - d)\) is 0. Since \(d\) is positive, we have: \begin{align} 2x - d &= 0 \\ 2x &= d \\ x &= \frac{d}{2} \end{align} As for \(y\), substitute the value of \(x = \frac{d}{2}\) back into the first equation and get: \begin{equation} y = \pm \sqrt{1 - \left(\frac{d}{2}\right)^2} \end{equation}
So the two circles will intersect at the points \(\left(\frac{d}{2}, \pm \sqrt{1 - \left(\frac{d}{2}\right)^2}\right)\). Please note the bounds of \(d\) are \begin{equation} 0 < d \le 2 \end{equation} Since \(1 - \left(\frac{d}{2}\right)^2\) will be less than 0 if \(d > 2\), which cannot be possible for a square root yielding a real value. In fact, when \(d = 2\), the circles only touch at one point, which is (1, 0).
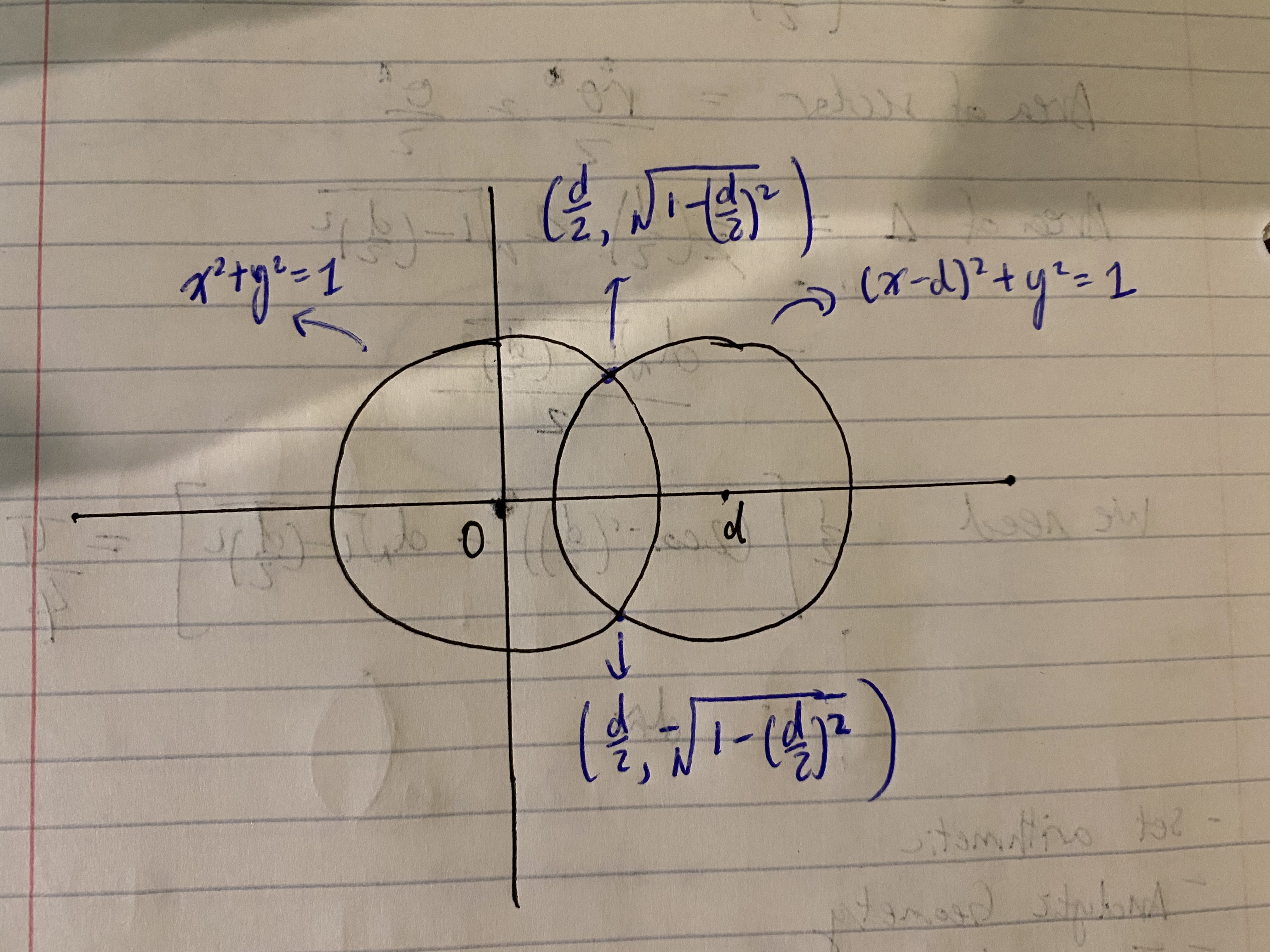
Once we've used analytic geometry to make sense of \(d\) in the context of the two circles, we can then use trigonometry to arrive at our answer based on the result of the set arithmetic section, which is that the area of the shaded region is \(\frac{\pi}{2}\). By symmetry, we just need to focus on one of the circles, since the other circle has the exact same size. Focusing on one circle, imaging a line \(x = \frac{d}{2}\) slicing down the shade region in the middle of the diagram shown above. It will divide the shaded region's area exactly in half. The region to the right of the vertical line, but still within the left circle, would have an area of \(\frac{\pi}{4}\). This, and combining the result from the previous section, we arrive at the following diagram:
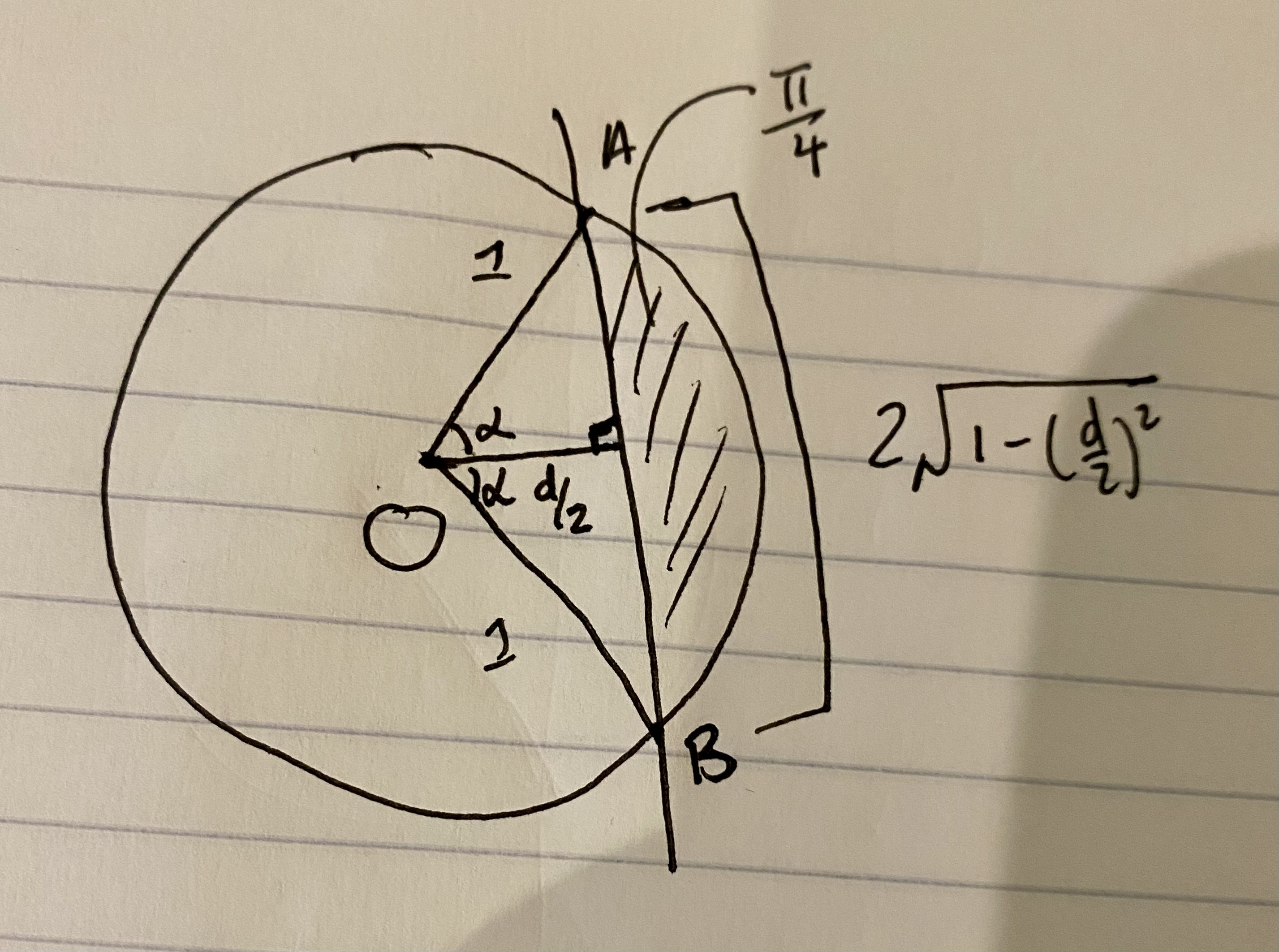
Now our strategy becomes clear: We can write the area of the sector \(OAB\) in terms of \(d\), as well as write the area of triangle \(OAB\) in terms of \(d\). We know that the difference between the former and the latter is \(\frac{\pi}{4}\), so we can use it to solve for \(d\)! In other words: \begin{equation} \text{Area of sector} OAB - \text{Area of triangle} OAB = \frac{\pi}{4} \end{equation}
For the sector, the angle subtended by chord \(AB\) is denoted as \(2\alpha\), where \(\alpha\) is the angle of each of the halved right-angled triangles. Since the circle has radius 1, the hypotenuse of the right-angled triangle is 1 as well. One of its sides has length \(\frac{d}{2}\) from the previous step, and so we use trigonometry to see that: \begin{align} \cos{\alpha} &= \frac{\text{adjacent}}{\text{hypotenuse}} \\ &= \frac{d/2}{1} \\ &= \frac{d}{2} \\ \alpha &= \arccos{\frac{d}{2}} \end{align}
Therefore, the angle subtended by chord \(AB\) is \(2\alpha = 2\arccos{\frac{d}{2}}\). The formula for the equation of sector is: \begin{equation} \text{Area of sector} = \frac{\theta r^2}{2} \end{equation} Where \(\theta\) is the angle subtended by the chord, which we have just derived in this case to be \(2\alpha\). So the area of our sector here is: \begin{equation} \text{Area of sector} = \frac{2\arccos{\frac{d}{2}}}{2} = \arccos{\frac{d}{2}} \end{equation} Don't forget that \(r = 1\) here.
For the triangle, we have the height and base from the analytic geometry derivation, so we have: \begin{align} \text{Area of triangle} &= \frac{1}{2} \times \text{base} \times \text{height} \\ &= \frac{1}{2} \frac{d}{2} 2 \sqrt{1 - \left(\frac{d}{2}\right)^2} \\ &= \frac{d}{2} \sqrt{1 - \left(\frac{d}{2}\right)^2} \end{align}
Putting everything together: \begin{align} \text{Area of sector } OAB - \text{Area of triangle } OAB &= \frac{\pi}{4} \\ \arccos{\left(\frac{d}{2}\right)} - \frac{d}{2} \sqrt{1 - \left(\frac{d}{2}\right)^2} &= \frac{\pi}{4} \\ \end{align}
Let's finally solve for \(d\)!
Once we have the equation for \(d\), we can solve it, by leveraging advances in computational technology. Here, courtesy of Wolfram Alpha, we can input our one equation with one unknown to get a numerical answer:

The two centers are about 0.8079 unit apart. (did you initially guess 1?)