



January 23, 2022
For full description of this geometry puzzle, please see the original puzzle here.
\(\frac{1}{13}\)
Explanation:
In the original puzzle we are given the following figure:

It has been told that the large hexagon is a regular one with side length 1 and it is inscribed within a circle. The "gap" between the top of that hexagon and the top of the circle circumscribes another smaller regular hexagon. What is the side length of that smaller hexagon?
Perhaps the following figure will shed some light:
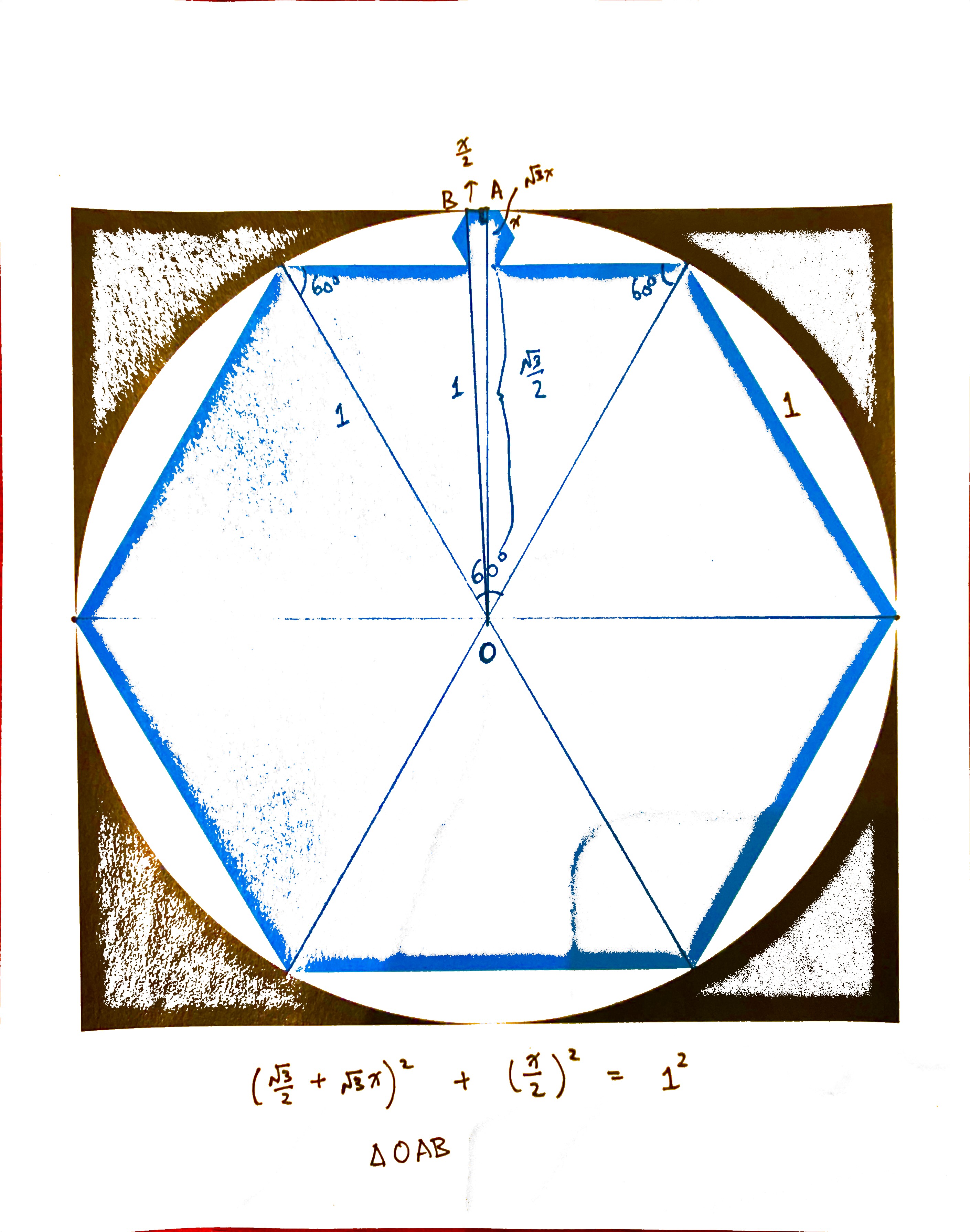
It turns out if we construct the right triangle (pun intended), we can easily arrive at the solution. The key is getting \(\Delta OAB\) as shown in the above image. We let \(x\) denote the side length of the smaller hexagon. Then, we claim that \(OB = 1\), \(OA = \frac{\sqrt{3}}{2} + \sqrt{3}x\), and \(AB = \frac{x}{2}\). From there on, it is a simple application of the Pythagorean Theorem: one unknown, one quadratic equation, ignoring the negative solution, and voila!
How did we get there? Well, let's take it one step at a time. First of all, the larger regular hexagon, by symmetry, can be divided into six congruent equilateral triangles, each of which having side length 1. Then, realizing that the hexagon is inscribed in a circle, then the center of that hexagon is also the center of the circumscribed circle, denoted as \(O\). Furthermore, any line segment connecting \(O\) to a point on the circle shall be its radius. Well, conveniently, such line segments exist as sides of the congruent equilateral triangles. From here we know that the radius of the circumscribed circle is 1. Then, realizing that \(OB\) is also a radius of the circle, its length is therefore 1.
What about \(AB\)? By symmetry, as the smaller hexagon sits right "on top" of the larger hexagon, its axis of symmetry bisects one of its sides, which has length \(x\). Hence, \(AB= \frac{x}{2}\).
Finally, for \(OA\), it is made up of two shorter segments: one from \(O\) to the side of the larger hexagon, and the other from the side of the smaller hexagon touching the larger one to its opposite side. For this we make use of a very important triangle: the 30-60-90 triangle. The diagram below shows the ratios of the sides of this special right-angled triangle:

Recall that the median of an equilateral triangle is also its altitude. Therefore, the "half-triangle" formed by bisecting an equilateral triangle, such as ones seen in the puzzle inside the regular hexagon, is a 30-60-90 triangle.
For the large hexagon, the side length is given as 1, and it corresponds to the hypotenuse of the 30-60-90 triangle. Therefore, the altitude is the long side, or \(\frac{\sqrt{3}}{2}\). For the small hexagon, the side length is given as \(x\), and so the altitude is given as \(\frac{\sqrt{3x}}{2}\). However, there are two altitudes as we are considering the distance across two opposite sides, and therefore, the segment's total length is twice that, or \(\sqrt{3}x\). Putting everything together, we have \(OA = \frac{\sqrt{3}}{2} + \sqrt{3}x\).
Pythagorean Theorem says:
\begin{align} OA^2 + AB^2 &= OB^2 \end{align}
Therefore, we have:
\begin{align} OA^2 + AB^2 &= OB^2 \\ \left(\frac{\sqrt{3}}{2} + \sqrt{3}x\right)^2 + \left(\frac{x}{2}\right)^2 &= 1^2 \\ \frac{3}{4} + 3x + 3x^2 + \frac{x^2}{4} &= 1 \\ 3 + 12x + 12x^2 + x^2 &= 4 \\ 13x^2 + 12x - 1 &= 0 \\ 13x^2 + 13x - x - 1 &= 0 \\ 13x(x + 1) - (x + 1) &= 0 \\ (13x - 1)(x + 1) &= 0 \\ x = \boxed{\frac{1}{13}} \quad \text{or} \quad x = -1 \\ \end{align}
Ignoring the negative solution, the side length of the smaller hexagon is \(\boxed{\frac{1}{13}}\).
From the image, it is very tempting to conclude that the distance between the two opposite sides of the small hexagon is the entire gap between the large hexagon and the circle. However, it is not so as there is a microscopic gap between the small hexagon and the top of the circle. Just exactly how small?
\begin{align} &\text{Gap} \\ &= 1 - \left(\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{13}\right) \\ &= 1 - \sqrt{3}\left(\frac{15}{26}\right) \\ &= \boxed{\frac{26 - 15\sqrt{3}}{26}} \\ &\approx 0.00074 \end{align}
The tiny gap makes up less than 0.1% of the entire radius of the circle.
The puzzle then asked to fit not one but two even smaller hexagons inside that tiny less-than-0.1% gap. What are the lengths of those hexagons?

The method of solving the first small hexagon provided a blueprint to set up similar right-angled triangles in solving for the subsequent smaller ones. Letting their side lengths be \(x\), we will always have the short side as \(\frac{x}{2}\). The hypotenuse is always the radius, being 1, and finally, the long side is going to be the total lengths of the individual long side segments of the hexagons before it plus \(\sqrt{3}x\). The second smaller hexagon will therefore yield the following equation after applying the Pythagorean Theorem.
\begin{align} \left(\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{13} + \sqrt{3}x\right)^2 + \left(\frac{x}{2}\right)^2 &= 1^2 \\ x = \boxed{\frac{1}{13(90 + \sqrt{8113})}} \quad \text{or} \quad x = -\left(\frac{90}{169} + \frac{\sqrt{8113}}{169}\right) \\ \end{align}
Ignoring the negative solution, the side length of the second smaller hexagon is \(x = \boxed{\frac{1}{13(90 + \sqrt{8113})}} \approx 0.000427\). At this point the gap is approximately \(2.28 \times 10^{-8}\).
In this gap, we are to create another, even smaller hexagon. The exact value of that hexagon is given by the following quadratic equation set up via Pythagorean Theorem using similar approaches as above.
\begin{align} \left(\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{13} + \frac{\sqrt{3}}{13(90 + \sqrt{8113})} + \sqrt{3}x\right)^2 + \left(\frac{x}{2}\right)^2 &= 1^2 \\ \end{align}
The positive solution is: \(\frac{1}{13(1460250 + 16212\sqrt{8113} + \sqrt{4264661495941 + 47347148340\sqrt{8113}})}\) which is approximately \(1.317 \times 10^{-8}\). This means the gap shortens by \(\sqrt{3}\) times that amount, resulting in approximately \(\boxed{5.51 \times 10^{-17}}\). Keep in mind the original radius of the circumscribed circle is 1.
Putting this distance in context, imagine a table with this hexagonal repeating pattern, where the circle making up the face of the table has radius 1. Then, the gap between the top of the circle and the third smaller hexagon being \(5.51 \times 10^{-17}\) means that it is more than 670,000 times smaller than the width of a hydrogen atom. This gap is as small compared to a hydrogen atom as a dust mite is compared to Burj Khalifa, the tallest structure in the world.