



January 27, 2023
The #blindletterchallenge has recently taken TikTok by storm. In this challenge, you are presented with five letters, one at a time. Letters are picked randomly, but you can assume that no two letters are the same (i.e., letters are picked without replacement). As each letter is presented, you must identify which of five slots you will place it. The goal is for the letters in all five slots to be in alphabetical order at the end.
For example, consider an attempt at the challenge by Michael DiCostanzo. The first letter is X. Since this occurs relatively late in the alphabet, he puts this in the fifth slot. The second letter is U. He puts that in the fourth slot, since it also comes relatively late (and the fifth slot is already occupied). Next, the third letter is E. He takes a gamble, and places E in the first slot. The fourth letter is D. Since D comes before E alphabetically, but no slots prior to E are now available, Michael loses this attempt.
If you play with an optimal strategy, always placing letters in slots to maximize your chances of victory, what is your probability of winning?
Theoretical maximum winning percentage is 25.43%. The lower bound by strategy described in this blog is 24.14%.
Explanation:
The best strategy involves ensuring the optimal placement of letters within the appropriate interval such that it evens out the number of letters per remaining slot and thereby reducing the cases of failure. As an extreme example, consider the letter 'R' being the first picked letter. One would not place 'R' in the first slot since it leaves at most eight letters to be placed in the subsequent four slots with two letters per slot on average. If 'R' is placed last, then it leaves 17 letters among the first four slots with just over 4 letters per slot. Placing 'R' in the fourth slot leaves 17 letters among the first three slots for just about 8 letters per slot and leaving 8 letters for the last slot just after 'R'. Clearly, the third placement strategy leaves greatest option for the subsequent letters.
One decent way to approximate the above strategy mathematically is to think of evenly dividing the available spaces to place the letters in quantiles. For simplicity, let's think of the letter challenge as a number challenge (since this is a math blog, why not?). Please note that unlike writing a novel, there is nothing special about each letter and we assume each letter is equally likely to be picked among the unpicked ones. Therefore, this challenge is equivalent of picking five integers without replacement from 1 to 26, inclusive. There are five ordered slots, and we place each picked number in one of the empty slots such that in the end the five numbers are in ascending numerical order. The algorithm is as follows:
For a chosen number, we find the interval where that number can be placed. An interval here is a set of consecutive slots between a filled slot and/or the first/last slot where the number can go. Let the alphabet size be \(N\), and let the first slot be bounded by \(x = 0\) and the last slot be bounded by \(y = N + 1\). Let an interval be \([x_0, x_1]\) and define the interval range \(r = (x_1 - x_0 - 1)\). Define \(n\) as the number of slots in that interval. Then, each slot in the interval \([x_0, x_1]\) can take \(\frac{r}{n}\) numbers, and we can divide the numbers distributions evenly. A new number, \(s\), to be placed in interval \([x_0, x_1]\) is to be assigned in the correct quantile as mathematically described below:
\begin{align} \text{slot number} &= k \\ &= \left \lceil (s - x_0) \times \frac{r}{n} \right \rceil \\ \end{align}
Where \(\lceil x \rceil\) is the ceiling function on \(x\). If there are \(n\) slots in an interval, then \(s\) should be placed \(k\) slots after \(x_0\).
If at any point we cannot find the appropriate interval in step 1, then we fail the challenge.
We now run our optimal strategy for the original challenge, with \(N = 26\) and number of starting slots as 5. We have using MATLAB:
function res = doTheLetterChallenge(n)
% 26 Numbers doing the letter challenge with n starting slots.
% return true if challenge successful and false otherwise
alphabetSize = 26;
slots = [0 NaN(1, n), alphabetSize + 1];
alphabet = 1:alphabetSize;
fill = 0;
while fill < n
% We pick a new number and calculate the interval
num = pickNumber(alphabet);
% Update the alphabet to remove the picked number from it
alphabet = alphabet(alphabet~=num);
% caluclate interval
[x0, x1, left, right] = calculateInterval(num, slots);
% First see if we have the space, otherwise the challenge fails
if right - left <= 1
% No space left
res = 0;
return;
end
% Next we place the new number
range = x1 - x0 - 1;
numSlots = right - left - 1;
k = ceil((num - x0) * (numSlots/range));
slotIdx = left + k;
% Update the slot
slots(slotIdx) = num;
% increment fill
fill = fill + 1;
end
res = 1;
end
This is a top-down approach of the code on doing the challenge using the approximation of the best strategy. Individual steps are as follows:
function [x0, x1, left, right] = calculateInterval(num, slots)
% find the interval for num given the slots
% slot numbers are sorted in ascending order bounded by 0, N + 1
left = 1;
right = length(slots);
leftAdv = left;
rightAdv = right;
leftStop = false;
rightStop = false;
while ~leftStop || ~rightStop
% look at left side
if ~leftStop
leftAdv = leftAdv + 1;
while(isnan(slots(leftAdv)))
leftAdv = leftAdv + 1;
end
if slots(leftAdv) < num
left = leftAdv;
else
leftStop = true;
end
end
% Now look at the right side
if ~rightStop
rightAdv = rightAdv - 1;
while(isnan(slots(rightAdv)))
rightAdv = rightAdv - 1;
end
if slots(rightAdv) > num
right = rightAdv;
else
rightStop = true;
end
end
end
x0 = slots(left);
x1 = slots(right);
end
function num = pickNumber(alphabet)
len = length(alphabet);
pickIdx = randi(len);
num = alphabet(pickIdx);
end
As sanity check, the challenge always passes for \(n = 1\) and \(n = 26\). In the former case, you only have one number (letter) and it will always be in order. For the latter case, every number can be assigned to its place in order since all numbers are to show up.
With 10 million trials, this yields a winning rate of 24.14%.
Using dynamic programming, once we picked a number in the slot, we partition the slot into two sub-slots and play two subgames within those slots. The literature figure is apparently 25.43%, though it is not clear what strategy achieves that value. The above strategy comes very close to it, as a curious observation.
A curious question one can ask is: "if we increase the number of slots, do our chances of winning decrease?". The short answer is yes--up to a point. Then, the probability of winning actually increases a bit. This is because as the number of slots increase, the optimal slots that a new number can go decreases, to a point where you just map it to the slot number and leave the rest to chance. When the number of slots reach 26, you are guaranteed to win.
Below is the probabilities of winning for each slot, with 1 million Monte-Carlo simulations using MATLAB.
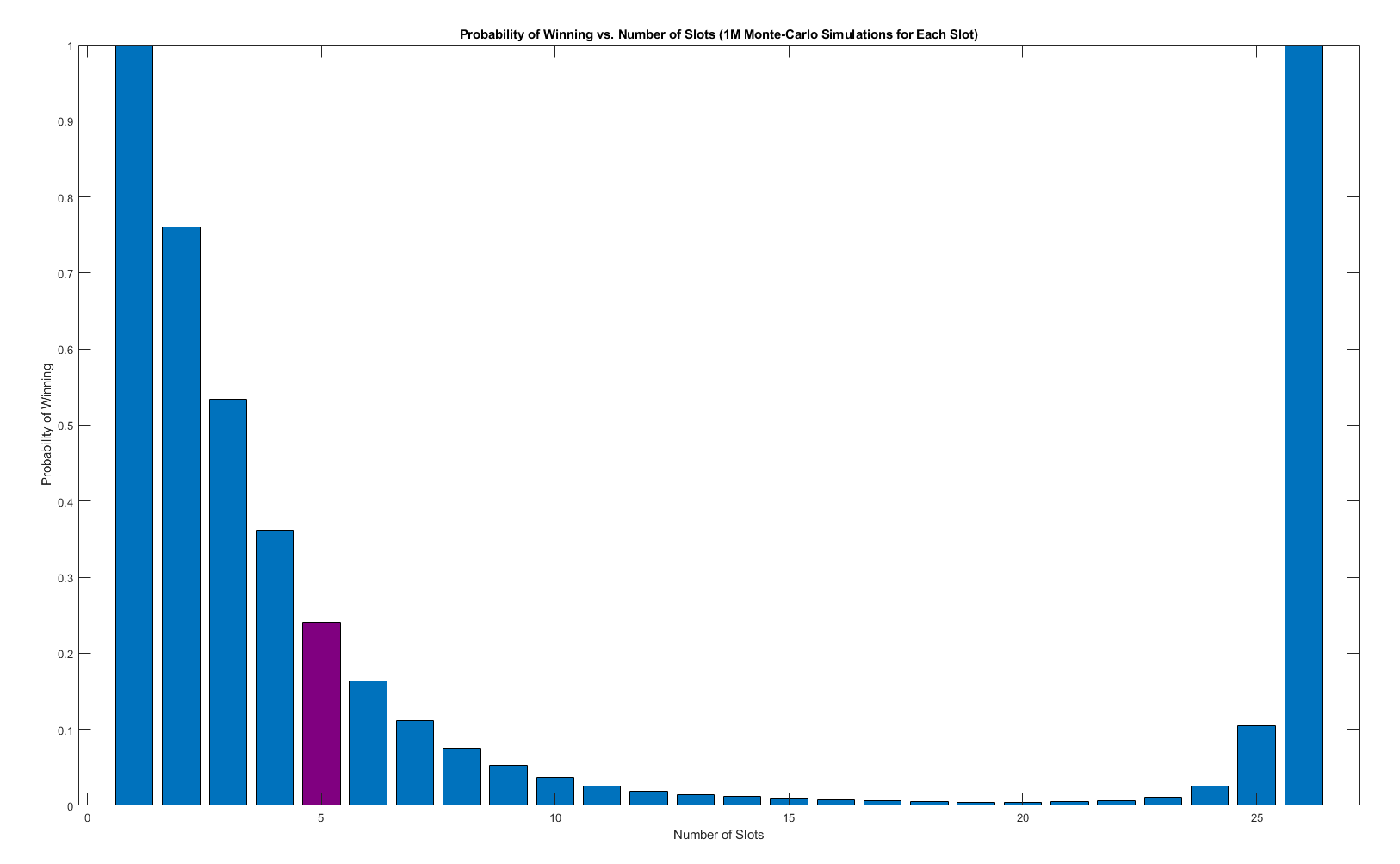
From the figure above, the hardest challenge is actually 20 slots, with a probability of winning using the described strategy to be just about 0.45%. Please note that the probability of winning returns to 1 as number of slots reaches 26.