



February 7, 2021
From Toby Berger comes a towering challenge:
Cassius the ape (a friend of Caesar’s) has gotten his hands on a Lucas’ Tower puzzle (also commonly referred to as the “Tower of Hanoi”). This particular puzzle consists of three poles and three disks, all of which start on the same pole. The three disks have different diameters — the biggest disk is at the bottom and the smallest disk is at the top. The goal is to move all three disks from one pole to any other pole, one at a time, but there’s a catch. At no point can a larger disk ever sit atop a smaller disk.
For N disks, the minimum number of moves is \(2^N - 1\). (Spoiler alert! If you haven’t proven this before, give it a shot. It’s an excellent exercise in mathematical induction.)
But this week, the minimum number of moves is not in question. It turns out that Cassius couldn’t care less about solving the puzzle, but he is very good at following directions and understands a larger disk can never sit atop a smaller disk. With each move, he randomly chooses one among the set of valid moves.
On average, how many moves will it take for Cassius to solve this puzzle with three disks?
Extra credit: On average, how many moves will it take for Cassius to solve this puzzle in the general case of N disks?
Answer: Read on until the end!

Explanation:
This will perhaps be one of my most comprehensive Riddler solution posts to date. I will take my reader on a journey into my thought process from the initial gathering of intuition to the final analytic generalization of the \(N\) disks case. This puzzle has presented me an opportunity to brush up on my algorithms skills, induction, and linear algebra, in which I am grateful for the puzzle creator.
In order to understand the puzzle setup, it is helpful to go through the exercise of proving the minimum required moves for the Tower of Hanoi with \(N\) disks being \(2^N - 1\). The proof is as follows.
If \(N = 1\), clearly it takes \(2^1 - 1 = 1\) move to solve the puzzle, as one can simply move the disk from the starting pole to the end pole in one fell swoop. Assume this also holds for \(N = k\). That is, we assume, as the induction hypothesis, that it takes \(2^k - 1\) moves at minimum to solve the Tower of Hanoi puzzle with \(k\) disks. Then, for the puzzle with \(k+1\) disks, the general strategy would be to move the first \(k\) layers of the disks onto the second, placeholder pole, then move the last disk onto the end pole, and then proceed to move the \(k\) disks from the placeholder pole onto the end pole. Throughout this process no moves will be illegal, because the largest disk is always at the bottom of the poles, and so the first \(k\) disks can be moved as if the largest, \((k+1)\)st disk, is not there. The total number of moves would hence be:
\begin{align} \text{Total Moves} &= (2^k - 1) + 1 + (2^k - 1) \\ &= 2(2^k - 1) + 1\\ &= 2^{k+1} - 2 + 1\\ &= 2^{k+1} - 1 \end{align}
The first line is exactly our strategy: spend the minimum amount to move the \(k\) disks onto the placeholder pole, which by symmetry is no different than moving those disks onto the end pole, then spend one move moving the largest disk directly from the starting pole to the end pole, then finish by moving the \(k\) disks from the placeholder pole onto the end pole, again by symmetry no different than moving from another pole. Re-arranging the expression yields \(2^{k+1} - 1\), which by the principles of mathematical induction, shows the minimum required moves for solving Tower of Hanoi with \(N\) disks is \(2^N - 1\).
Unfortunately, the Riddler puzzle is asking the average number of moves that our simian friend Cassius is expected to take to solve the puzzle. Cassius will randomly make any legal move at all stages of the puzzle. After understanding what the tower is about, I wrote a simulation program to emulate Cassius' actions, in MATLAB, of course.
(Note: I've uploaded all my code to my GitHub account, which I will share at the end of the post. For now, I will share code snippets depending on the context.)
function moves = getNumMoves(N)
% One simulation of number of moves to solve the Tower of Hanoi of N
% disks.
% Note: the minimum moves required is 2^N - 1
% The tower is represented as an N by 3 matrix. An entry with a
% non-zero indicates the presence of a disk, and 0 otherwise. The
% first column shall be the starting column and the last column being
% the final (goal) column. In any column, no non-zeros can be below any
% other non-zeros of greater value.
tower = zeros(N, 3);
tower(:, 1) = (1:N)';
moves = 0;
% Now we start to count the moves
while ~isTowerSolved(tower)
moveList = populateMoves(tower);
numPosMoves = length(moveList);
moveLotto = randperm(numPosMoves); % Shuffle the moves
moveIdx = moveLotto(1);
tower = moveList{moveIdx};
moves = moves + 1;
end
end
My representation of the tower is very simple: an N by 3 matrix. Each entry is either a 0 or a number representing the size of the disk. Using this setup, I can populate the list of possible moves given the current state of the tower, and then use the "randperm" function to shuffle up all of the possible moves and pick one with equal probability. Then I update the tower from the chosen move and repeat until the puzzle is solved! I keep count of the moves taken and run a Monte Carlo.
Here are my Simulation Results:
| \(N\) | Simulated Expected Number of Moves | Simulation Count |
| 1 | 2.003 | 1 million |
| 2 | 21.3442 | 1 million |
| 3 | 141.2463 | 1 million |
| 4 | 809.7995 | 20942 |
I had to cut the simulation short for \(N = 4\) because the complexities simply grew too fast--exponentially, in fact. However, the pattern I am receiving is indicative that the expected number of moves is also growing exponentially, which is expected as the moves are tied closely with the number of possible tower states.
For \(N = 3\) case, which is the focus of the puzzle, below is the frequency diagram of moves for each trial:

From the flame-like distribution it can be seen that periodically Cassius hits the jackpot and solves the puzzle in relatively fewer moves. However, at other times, it hits no such luck and moves go into the thousands. The move distribution is as follows:

Below are the key statistics:
| Minimum | 7 (As expected) |
| Maximum | 1657 |
| Mean | 141.2463 |
| Mode | 37 |
| Median | 103 |
So we have our sanity checks. Now I will venture into getting an analytical answer.
The different states of the Tower of Hanoi can be tied together through Markov Chains. We know from the puzzle that transitioning from one state of the tower to another is either 0 if the transition is impossible in one move, or \(\frac{1}{\text{Possible Moves}}\) since Cassius randomly chooses a legal move to make. Furthermore, we know that the end state is always when all of the disks end up on the end pole, in which we will stay in that state. In the context of the Markov Chain, this will be the sole recurring state of the chain. We can tie everything into a Markov Chain with transition probability matrix \(P\), in the following form:
\begin{equation} P = \left[ \begin{matrix} Q & R \\ 0 & 1 \end{matrix} \right] \end{equation}
Where Q represents the transition probability in the transient states. Once the tower reaches the end state, it transits to itself with probability of 1 and other states with probability of 0 (hence the term recurring). This is represented by the last row of the transition matrix \(P\). In this case, we have only 1 recurring state as the Tower of Hanoi has only one solution, and hence if there are \(N\) disks, there will be \(3^N\) states (homework for my readers!). \(P\) will be a \(3^N \times 3^N\) matrix, and Q will be a \((3^N-1) \times (3^N-1)\) matrix.
Define \(F\), the fundamental matrix, as \((I - Q)^{-1}\), where \(I\) is the corresponding identity matrix, we can obtain a \((3^N-1) \times 1\) vector, called \(\overrightarrow{t}\), representing the expected number of transitions into the recurring state, as follows:
\begin{equation} \overrightarrow{t} = F \overrightarrow{1} \end{equation}
Where \(\overrightarrow{1}\) is the all-ones vector. The \(i\)th entry of vector \(\overrightarrow{t}\) represents the expected number of moves going from state \(i\) into the recurring state. Assuming the original tower configuration corresponds to state 1, the answer is found in \(\overrightarrow{t} (1)\).
An example of using the above Markov Chain to obtain an analytic answer for \(N = 1\) case is shown below:
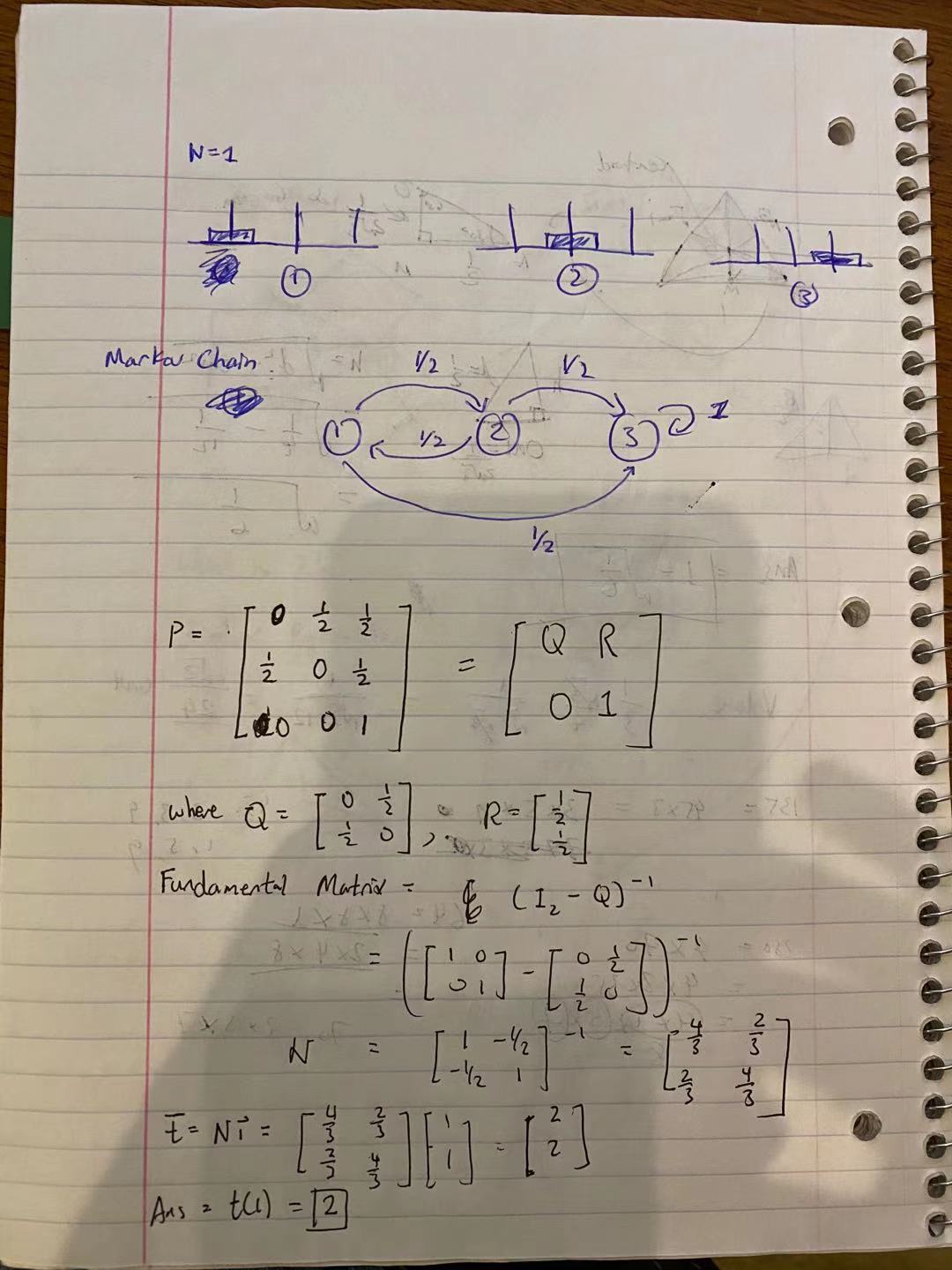
From the above we see that the analytic answer for \(N=1\) is 2. That is, for the one disk case, Cassius is expected to solve the puzzle in 2 moves. This is very close to our Monte Carlo result of 2.003.
Of course, as \(N\) increases, the number of cases and transitions to consider goes up exponentially. As such, it would not be practical to list everything on pen and paper. Luckily, I can exploit the recursive nature of the Tower of Hanoi and build an analytic solver, in MATLAB, that can in theory get the number of moves for any \(N\). I mentioned in theory because even the anlytical solver is subject to the growing complexities of the disks. Nonetheless, I built one, in which the source code is in my GitHub Repo in which I will share the link at the end. For now, I will reveal code snippets to illustrate how the solver works.
In a top-down approach, let me first show you the function to compute the expected number of moves, which is only a few lines:
function moves = getExpectedNumMoves(N)
% Analytic Calculation of expected moves for Tower of Hanoi of N disks.
states = towerStateGenerator(N);
numStates = length(states);
P = zeros(numStates, numStates); % P is the transition matrix
for i = 1:numStates
for j = 1:numStates
if canTransit(states, i, j)
P(i, j) = 1;
end
end
% Normalize the row
sumTransit = sum(P(i, :));
if sumTransit > 0
P(i, :) = P(i, :)/sumTransit;
end
end
% Now it's just linear algebra and Markov Chain theory
Q = P(1:numStates-1, 1:numStates-1);
F = (eye(numStates-1) - Q);
tVec = F\ones(numStates-1, 1);
moves = tVec(1);
end
The meat of the solver, of course, lie inside the "towerStateGenerator" and "canTransit" functions. The former creates all \(3^N\) states of the tower and the latter takes in two states and determine whether one can transition into the other. The states are built up recursively, as follows. See if you can catch the recursive step:
function states = towerStateGenerator(N)
% This function returns a cell array of all possible states in a Hanoi
% Tower configuration of N disks.
% Recursion will be used.
if N == 1
states = {
[1 0 0];
[0 1 0];
[0 0 1];
};
return;
end
stateSize = N*3;
newStates = cell(stateSize, 1);
prevStates = towerStateGenerator(N - 1);
for k = 0:length(prevStates)-1
prevState = prevStates{k+1};
for j = 1:3
newState = [zeros(1, 3); prevState];
newState(1, j) = N;
downIdx = 1;
while downIdx < N && newState(downIdx + 1, j) == 0
% Ensure no gaps between disks
newState(downIdx + 1, j) = newState(downIdx, j);
newState(downIdx, j) = 0;
downIdx = downIdx + 1;
end
newStates{k*3 + j} = newState;
end
end
states = newStates;
end
From the above state generator, I have amended my tower model from the Monte Carlo stage, where now integer size is inversely proportional to disk size. This is done for the simplicity of the solver algorithm.
Next I implemented the "canTransit" logic.
function res = canTransit(states, i, j)
% Given the list of states, determine whether state i can transit to
% state j
% Conditions of transter:
% 1) One and only one disk moved
% 2) The moved disk is from the top of a pole
% 3) Destination pole has that disk being the top disk legally
if i == j
res = false;
return;
end
s1 = states{i};
s2 = states{j};
movePattern = (s1 ~= s2);
if sum(sum(movePattern)) ~= 2
% No disk or more than 1 disk moved
res = false;
return;
end
% Look at whether one of the moved disks is the top disk
moveVec = s1(movePattern); % Two by 1 vector in which one is non-zero
% The edge case of two disks "swapping" is also no good
if all(moveVec)
% Swap case: no good!
res = false;
return;
end
diskMoved = moveVec(moveVec ~= 0);
for pole = 1:3
[maxDisk, diskIdx] = max(s1(:, pole));
if maxDisk ~= diskMoved
continue;
end
% Pole is the original pole where the moved disk occurred. Ensure
% that it is the top disk
for i = 1:diskIdx-1
pos = s1(i, pole);
if pos ~= 0
res = false;
return;
end
end
break;
end
% Now look at the new state to ensure that the moved disk does not have
% any larger disks on top of it.
for pole = 1:3
[maxDisk, diskIdx] = max(s2(:, pole));
if maxDisk ~= diskMoved
continue;
end
% Pole is the original pole where the moved disk occurred. Ensure
% that it is the top disk and no smaller disk is beneath it.
% Size of disk is inversely ordered.
for i = 1:diskIdx-1
pos = s2(i, pole);
if pos ~= 0
res = false;
return;
end
end
for i = diskIdx+1:length(s2(:, pole))
pos = s2(i, pole);
if pos > diskMoved
res = false;
return;
end
end
break;
end
res = true;
end
Finally, the solver builds the transition probability matrix from the states and their transition probabilities, whereupon linear algebra and Markov Chain theory, as described from the previous section, is invoked to arrive at the final answer!
At last, I can reveal the answer of the puzzle based on using the solver. For \(N = 3\), the solver yielded the following expected moves: \(\frac{1274}{9} = 141.5556\).
And that's the answer!
***
For extra credit, I first ran the solver for \(N = 1, 2, \dots, 8\) before the time complexities became to overwhelming. For the first four values of \(N\) below are the comparisons to the ones from Monte Carlo:
| \(N\) | Analytic Result | Monte Carlo Result |
| 1 | 2 | 2.003 |
| 2 | 21.3333 | 21.3442 |
| 3 | 141.5556 | 141.2463 |
| 4 | 805.9259 | 809.7995 |
Looks like I passed the sanity check. Now I can graph the log of the expected moves for the eight values of \(N\) against \(N\), and if the moves grow exponentially as I had stated, then the log graph should be a positively-sloped line. Placing a line of best fit to it should lead to a good approximation of the closed form for expected moves in terms of \(N\).
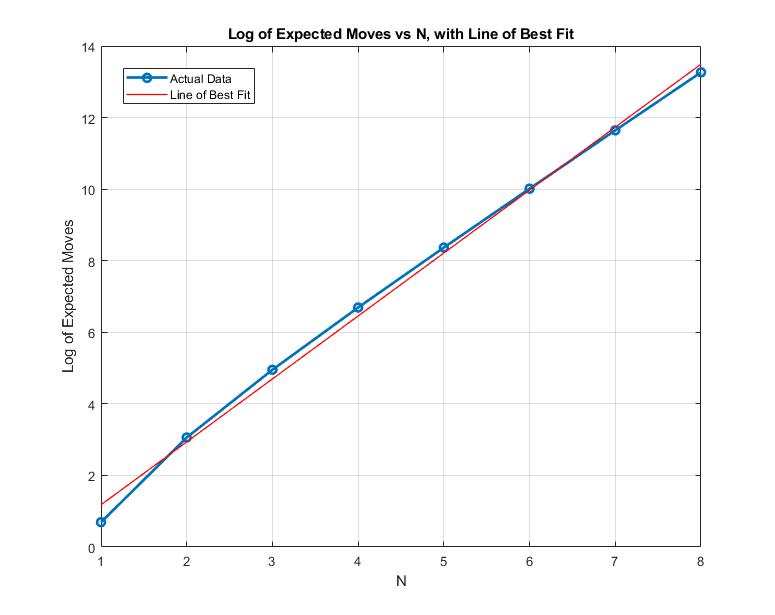
>> coefficients
coefficients =
1.7591 -0.5803
This yields: \begin{equation} f(N) \approx e^{1.7591N - 0.5803} \end{equation}
Please find all my code and results for this project on my GitHub Repo:
Courtesy of Steve Gabriel, there is a paper from 2014 that he unearthed, written by Max A. Alekseyev and Toby Berger, that provides the closed-form formula for N:
\begin{equation} f(N) = \frac{(3^N-1)(5^N - 3^N)}{2 \cdot 3^{N-1}} \end{equation}
For n=14 I get 4,574,047,435.86 moves. Inefficient matrix build time: 7 minutes. Actual sparse solve: 7 seconds. Of course this is more computational insanity given that there's a 2014 paper with analytic solution.https://t.co/qIGenbeGuA
— Steve Gabriel (@sg777) February 8, 2021