



April 19, 2021
This past Monday marked the beginning of Ramadan in the U.S. The month-long observance traditionally begins with the sighting of a crescent moon, or hilal, after a new moon. For this week’s Classic, let’s take a closer look at a waxing crescent moon.
After a new moon, the crescent appears to grow slowly at first. At some point, the moon will be one-sixth full by area, then one-quarter full, and so on. Eventually, it becomes a half-moon, at which point its growth begins to slow down. The animation below provides some insight into what’s happening here:

How many times faster is the area of the illuminated moon growing when it is a half-moon versus a one-sixth moon?
Solution:
First of all, I would like to wish a very Happy Ramadan to everyone around the world who celebrates it. Ramadan Mubarak!
As the crescent moon appears into view in the reddened western portion of the sky, lit up by the fading glows of the setting sun, our sole natural satellite begins a month-long transition of its illumination as viewed from Earth, otherwise known as a lunar phase. During this phase, how are the areas of the moon that we can see from our planet changes during this time? Before we dive in to solve this problem, we are going to make a few simplifying assumptions:
Oh and one more thing--we will now assume the Moon is a cylinder!
Alright, so obviously we know that the Moon is NOT a cylinder, and that this assumption is just a tad too far-fetched. Nonetheless, borrowing a tip from Hungarian mathematician George Pólya, to solve a tough puzzle, solve a simpler one first! Doing so will often help us highlight the important parameters of the puzzle and ascertain the key to solving the real thing! So here, by assuming that the Moon is a cylinder, we can focus on the main theme of the puzzle: the actual waxing of the moon. You see, a cylinder projects onto a 2D plane as a rectangle. As it's hight is constant, there is only one angle that controls the waxing in the Moon's phase: the azimuth angle. The other defining angle of an otherwise spherical moon would be irrelevant here. For a clarification of those two angles, please see the diagram below:

The Moon will be waxing in the azimuth direction. At new moon, \(\phi = -\frac{\pi}{2}\) and at full moon, \(\phi = \frac{\pi}{2}\).
Now let us define \(\phi\) as the azimuth angle. By our uniform circular motion assumption on the Moon, \(\frac{\mathrm d \phi(t)}{\mathrm d t}\) is a constant, by which we can call it as \(k\). Now, as we are only looking at the Half-Moon line straight-on, there is effect of parallax when looking at an angle from the side. To illustrate this, please see my hastily-made marker-on-paper-towel-roll demo below:

Clearly, as the camera remains fixed, the direction in which we view the angle formed by the two black lines on the top of the paper towel affects the apparent angle of the actual angle (that's a lot of angles!). My point is, if the angle viewed from the top of the paper towel is \(\phi_0\), then the apparent angle would be \(\phi_0 cos \phi\), where \(\phi\) is the azimuth angle formed by the observer's direct line of sight and the first of the two black lines further away from you from the demo above. This is an example of the parallax effect.
The waxing of this cylindrical Moon can therefore be defined as the following differential equation:
\begin{equation} \frac{\mathrm d A(t)}{\mathrm d t} = \cos{\phi}\frac{\mathrm d \phi(t)}{\mathrm d t} \end{equation}
In order to look at how fast the Moon is waxing when it's half-full as compared to when it's only \(f\) of the total area (for \(0 \leq f \leq 1\)), we apply the boundary conditions. When the moon is full, we have:
\begin{align} \text{Normalized Area} &= \int_{\phi = -\frac{\pi}{2}}^{\phi = \frac{\pi}{2}} \cos{\phi}\mathrm d \phi \\ &= \sin{\phi} \left.\right |_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\ &= 2 \end{align}
When it's \(2f\) waxed, we would have:
\begin{align} 2f &= \int_{\phi = -\frac{\pi}{2}}^{\phi = x} \cos{\phi}\mathrm d \phi \\ &= \sin{\phi} \left.\right |_{-\frac{\pi}{2}}^{x} \\ &= 1 + \sin{x} \end{align}
Solving for \(x\), we get \(x = \arcsin{(2f - 1)}\).
At half-moon, when we plug \(f = \frac{1}{2}\) into the above equation, we get \(x = 0\).
Therefore, putting everything together, the following expression is how many times the cylindrical Moon is waxing faster at half-moon than as compared to when it's at "f-moon", for \(0 \leq f \leq 1\), when viewed from the side of the cylinder. The difference in rates is purely due to parallax and if viewed from the top of the cylindrical Moon, the waxing rate would be constant.
\begin{align} \text{Parallax Wax} &= \frac{k\cos{0}}{k\cos{\arcsin{(2f - 1)}}} \\ &= \frac{1}{\sqrt{1 - (2f-1)^2}} \\ &= \boxed{\frac{1}{2\sqrt{f(1-f)}}} \quad \text{for } 0 \leq f \leq 1 \end{align}
The following triangular diagram might help visualize the derivation above:

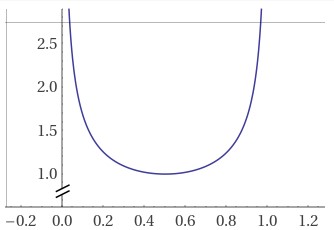
Below is a graph of how the increase in rate changes as we vary \(f\) from 0 to 1:
Okay not quite, but we will now make a relatively more realistic assumption that the Moon is a perfect sphere with radius \(r\). Here the only difference between the cylindrical Moon and its spherical counterpart would be that the latter requires another angle: the altitude angle in which we will denote as \(\theta\). The altitude angle \(\theta\) runs from \(-\frac{\pi}{2}\) to \(\frac{\pi}{2}\) and is independent of the waxing motion of the Moon (we assumed no wobbling of the Moon!), unlike that for the azimuth angle. The differential length at each altitude is given as \(r \cos{\theta} \mathrm d \theta\) as seen from trigonometry, instead of being constant for the cylindrical case. Once again, we must consider parallax effect in the altitude direction, but thankfully due to the symmetrical nature of the perfect sphere, the effect is the same as that for the azimuth direction. That is, the apparent angle is \(\cos{\theta}\) times the true angle. Putting everything together, the differential equation for the change of the spherical Moon's area with respect to time, as the Moon waxes, is:
\begin{align} \frac{\mathrm d A(t)}{\mathrm d t} &= \dots \\ &= \cos{\phi}\frac{\mathrm d \phi(t)}{\mathrm d t} \times \int_{\theta = -\frac{\pi}{2}}^{\theta = \frac{\pi}{2}} r^2 \cos^2{\theta} \mathrm d \theta \\ &= r^2 \cos{\phi}\frac{\mathrm d \phi(t)}{\mathrm d t} \times \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1 + \cos{2\theta}}{2} \mathrm d \theta \\ \frac{\mathrm d A(t)}{\mathrm d t} &= \boxed{\frac{\pi r^2}{2} \cos{\phi}\frac{\mathrm d \phi(t)}{\mathrm d t}} \end{align}
Wait a minute...the above differential equation is the SAME as that for the cylindrical case up to a constant co-efficient! It turns out that it didn't matter whether the Moon was cylindrical or spherical, so long as it only waxes in the azimuth direction, only \(\phi\) matters! Therefore, once again we have:
\begin{align} \text{Parallax Wax} &= \boxed{\frac{1}{2\sqrt{f(1-f)}}} \quad \text{for } 0 \leq f \leq 1 \\ \end{align}

Finally, to answer the question of the original puzzle, we substitute \(f = \frac{1}{6}\):
\begin{align} \text{Parallax Wax} &= \frac{6}{2\sqrt{5}} \\ &= \boxed{\frac{3\sqrt{5}}{5}} \\ & \approx 1.342 \end{align}
The rates are similar for the waning Moon case, but I guess "Parallax Wane" just doesn't have that ring to it.