



June 17, 2022
You have an urn with an equal number of red balls and white balls, but you have no information about what that number might be. You draw 19 balls at random, without replacement, and you get eight red balls and 11 white balls. What is your best guess for the original number of balls (red and white) in the urn?
The best guess is that there are 34 balls in the urn, with 17 red and 17 white. The probability of such selection is 16.2%.
Explanation:
Let the urn have \(N\) red and \(N\) white balls, for a total of \(2N\) balls. Clearly \(N \ge 11\). The probability of retrieving 8 red balls and 11 white balls without replacement is therefore:
\begin{align} \frac{\binom{N}{8} \binom{N}{11}}{\binom{2N}{19}} = \frac{\binom{19}{8} \binom{2N - 19}{N - 8}}{\binom{2N}{N}} \\ \end{align}
As \(N\) increases, both the numerator and denominator increases, so this suggests a "sweet spot" for \(N\) in which the probability is maximized, which will comprise our best guess for \(2N\). Using our friend MATLAB, we obtain:
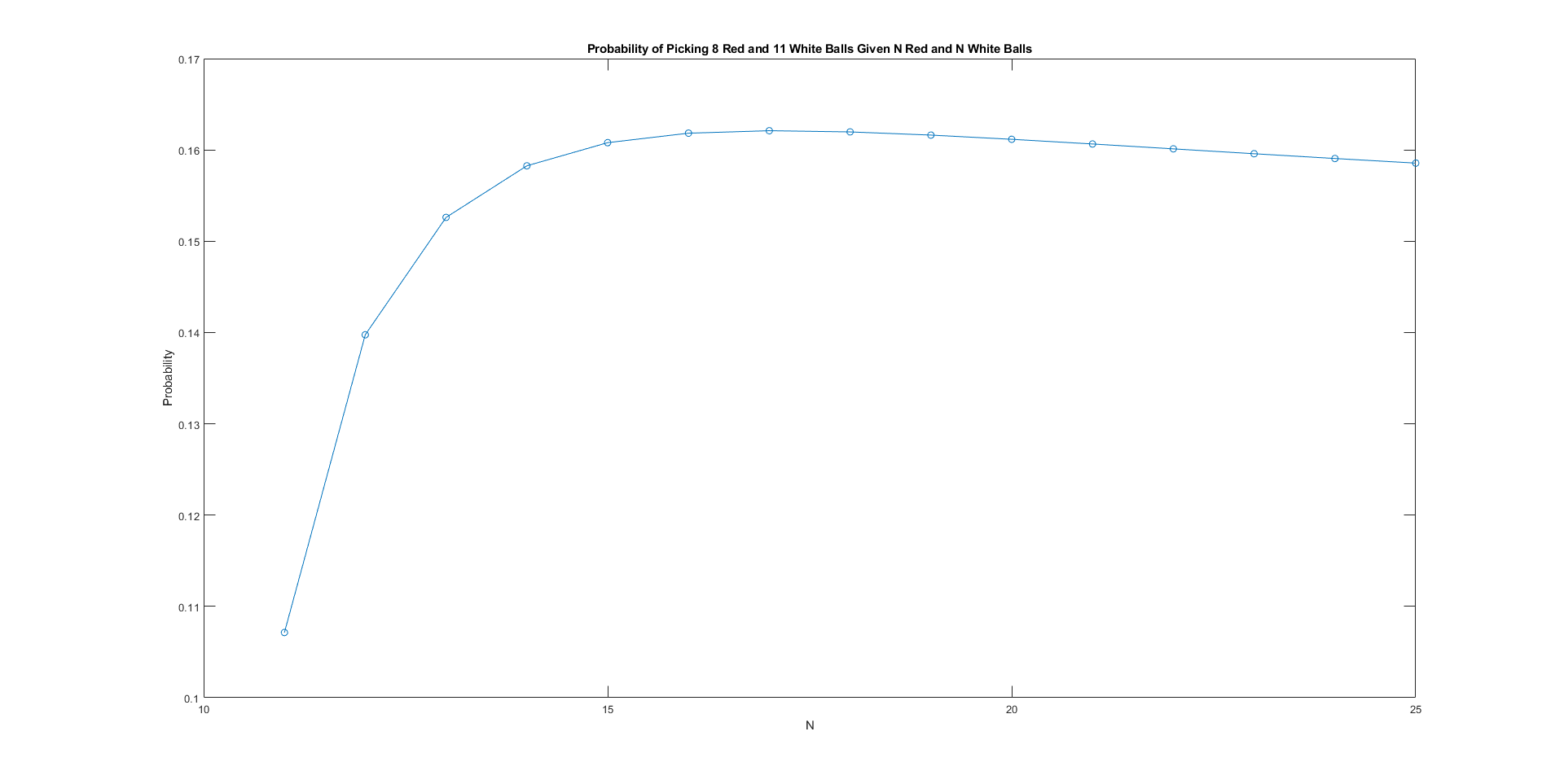
Upon further investigation, the probability increases drastically as \(N\) goes up from 11, before slowly dwindling down. The peak is at \(N = 17\):
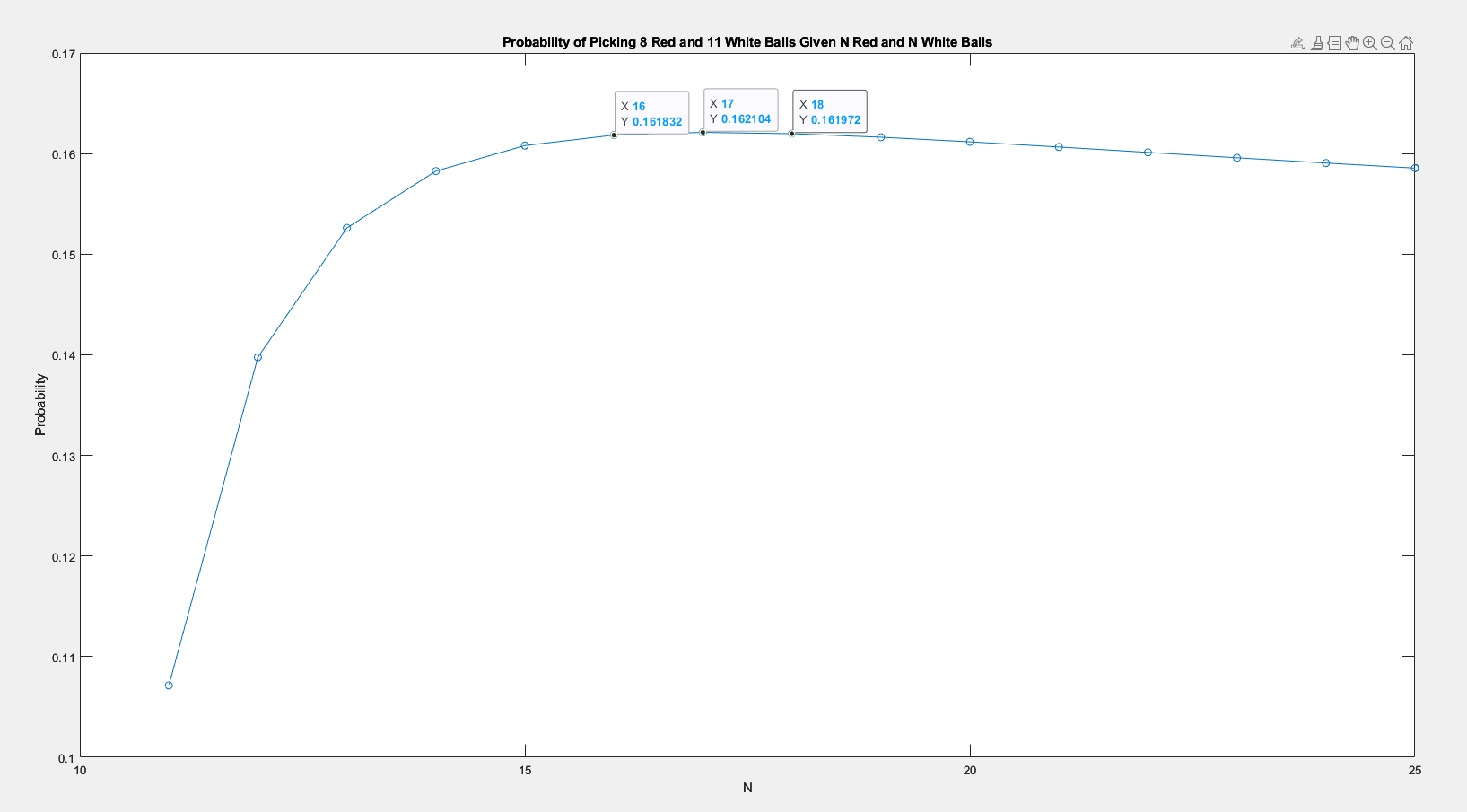
With 34 balls (17 red and 17 white), the probability of picking out 8 red and 11 white balls is around 16.2%.
Interestingly, if we instead picked out some balls such that we picked out \(m\) red and \(m\) white balls, then our best guess is that there are \(2m\) balls in the urn!
Proof:
Let there be \(N \ge m\) red and \(N \ge m\) white balls in the urn. Suppose we pick out exactly \(m\) red and \(m\) white balls, then the probability of doing so is:
\begin{align} \frac{\binom{N}{m} \binom{N}{m}}{\binom{2N}{2m}}\\ \end{align}
Setting \(m = N\), we obtain:
\begin{align} \text{Probability} &= \frac{\binom{N}{m} \binom{N}{m}}{\binom{2N}{2m}}\\ &= \frac{\binom{N}{N}^2}{\binom{2N}{2N}}\\ &= \frac{1}{1} = 1 \end{align}
Since by the axiom of probability the maximum value is 1, our best guess is that there are \(2m\) balls in the urn.