



June 24, 2022
A goat tower has 10 floors, each of which can accommodate a single goat. Ten goats approach the tower, and each goat has its own (random) preference of floor. Multiple goats can prefer the same floor.
One by one, each goat walks up the tower to its preferred room. If the floor is empty, the goat will make itself at home. But if the floor is already occupied by another goat, then it will keep going up until it finds the next empty floor, which it will occupy. But if it does not find any empty floors, the goat will be stuck on the roof of the tower.
What is the probability that all 10 goats will have their own floor, meaning no goat is left stranded on the roof of the tower?
From Monte-Carlo simulations, the answer is around 23.6%.
Explanation:
The solution to this riddle is via Monte-Carlo simulated using MATLAB, with 10 million trials each. I am happy to share the simulation code upon request. Feel free to reach out to me!
Let's first consider the original problem, whereby each goat randomly prefers one of the 10 floors. In this case, the Monte-Carlo simulation shows that 23.6% of the time no goat is stuck on the roof. In fact, the following is the distribution of number of goats stuck on the roof:
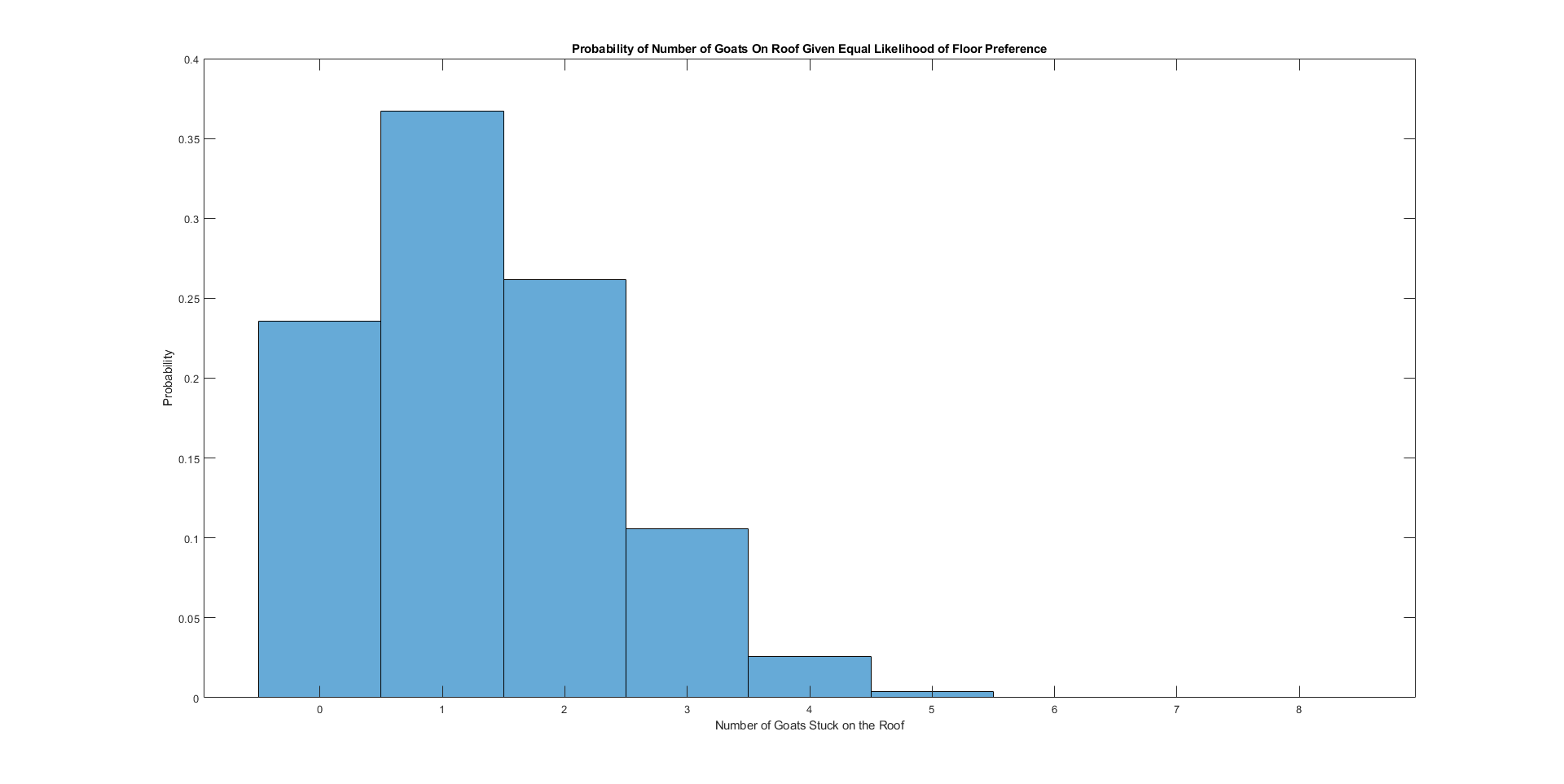
The mode is 1 goat stuck on the roof, happening about 36.7% of the time. This value is surprisingly close to
Interesting things occur for goats that prefer certain areas of the tower rather than wanting any floor with equal probability. In this section, we will explore the new likelihood of a goat being stuck on the roof, if goats prefer to stay on the lower floors. Intuition tells us that the probability of all goats finding a room in the tower will be much higher than with equal probability preference, because it is easier to fit a goat on a higher floor if the starting floor is closer to the ground. If a goat, say, prefers the 10th floor, and it is occupied, then the goat would have no choice but to go to the roof. However, if a goat prefers a lower floor, then even if it is occupied, there will be more floors to wiggle around finding a place for the goat.
We will assume now that the goats' floor preferences follows that of a Zipf distribution, which is a naturally occurring distribution with many scenarios involving discrepancies in popularity, such as frequency of letters in a novel. With this distribution, it is twice as likely for a goat to pick floor 1 than floor 2, and 3 times as likely to pick floor 3, and so on. Therefore, the lower the floor, the higher the probability for a goat to prefer it.
Let's see if our intuition is correct:
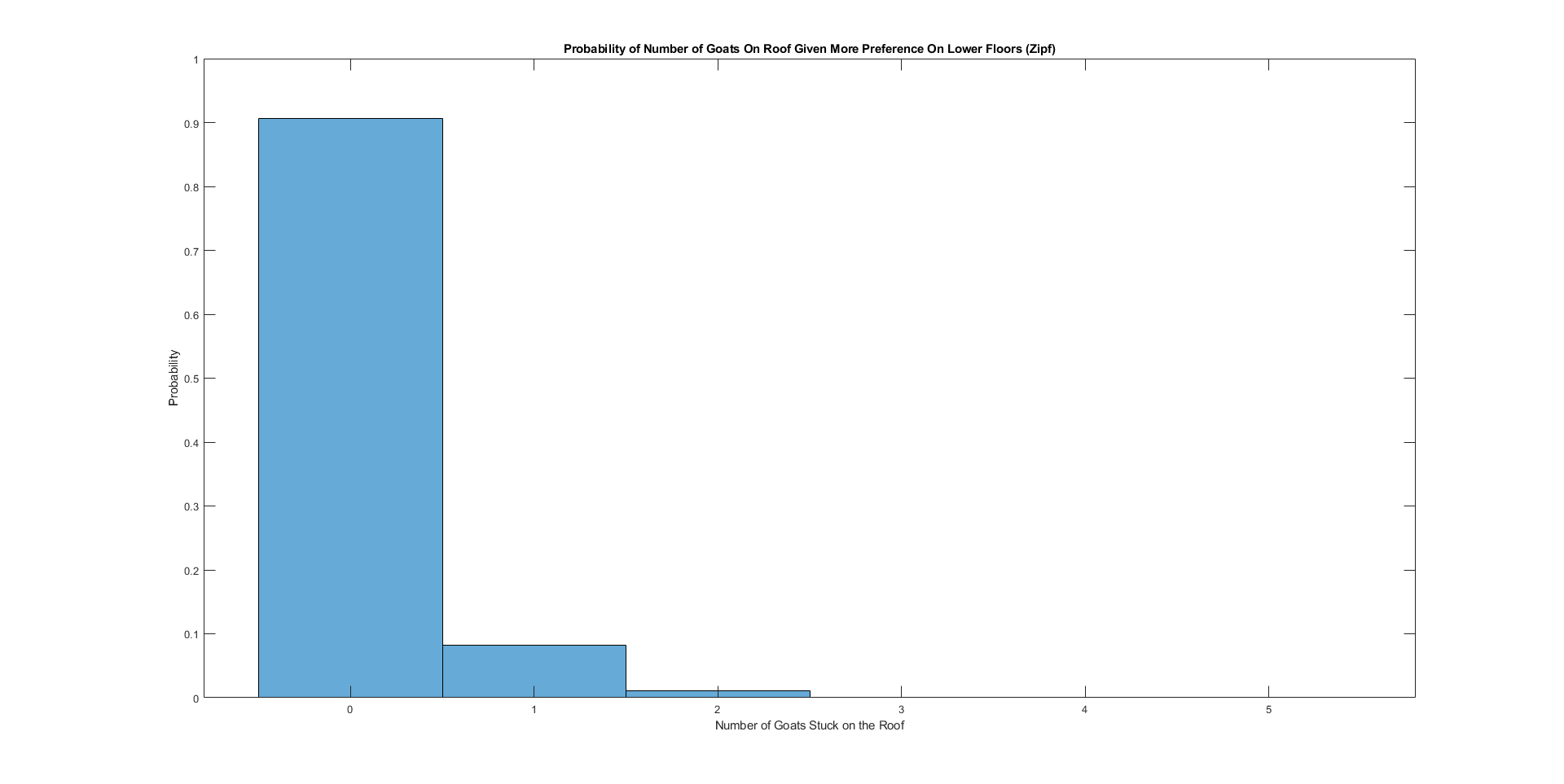
Indeed, 0 goats stuck on the roof clearly becomes the mode here. In fact, it occurs with a whopping 90.6% probability. The average number of goats stuck on the roof drops to a mere 0.107.
As alluded in the previous section, now we expect more goats, on average, to be stuck on the roof now that more goats want to occupy the higher floors. Once those floors are occupied, we have much fewer wiggle room, literally, to accommodate our ovine friends. Again, we will assume a Zipf distribution, except this time reversed from that of the previous section. That is, goats most prefer the 10th floor, twice as much as 9th, and three times as much as 8th, and so on.
Let's see if our intuition is correct once again:
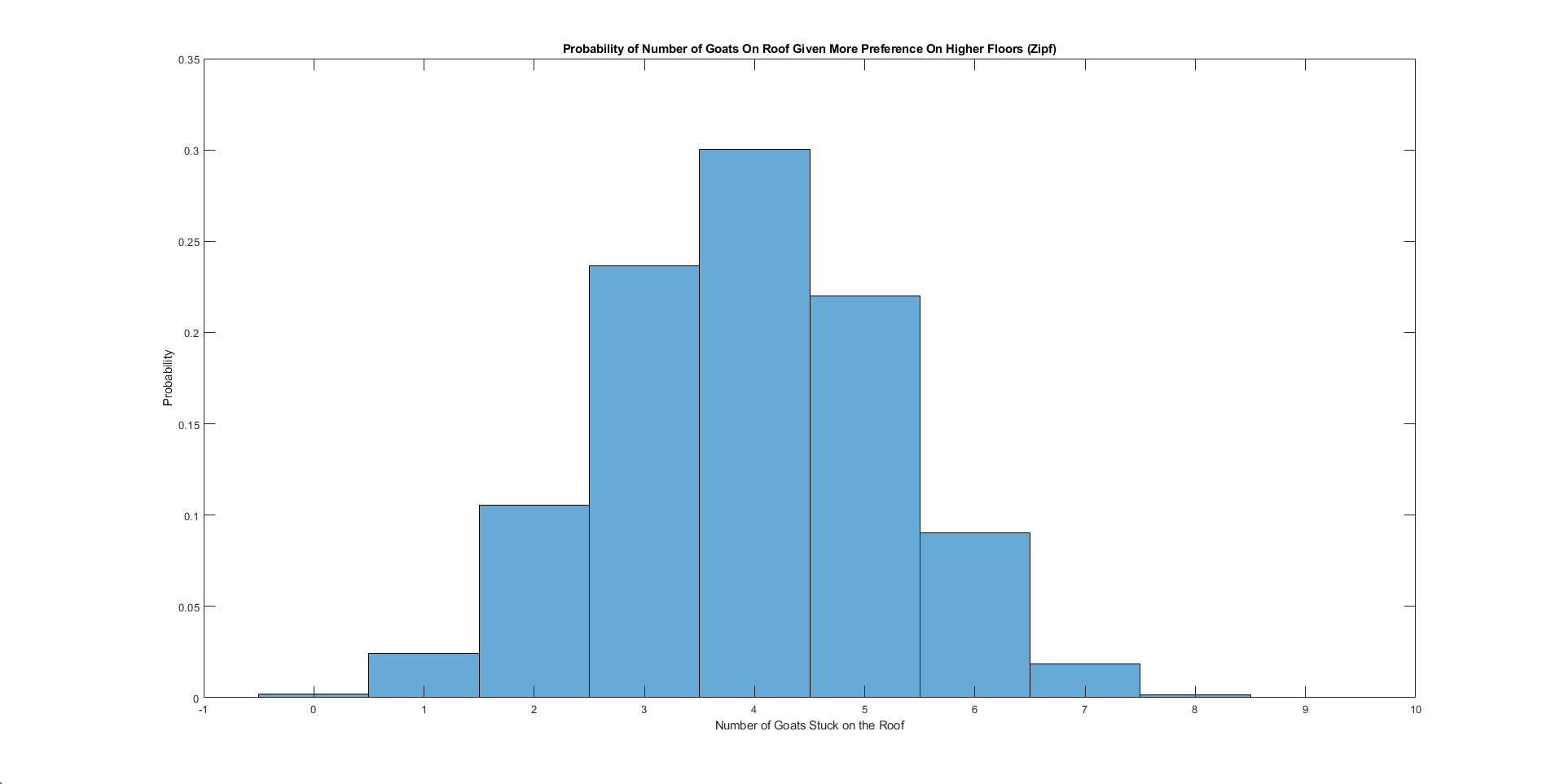
Now the curve shifts significantly to the right and in fact now resembles a normal distribution. The centering number appears to be 4, which is also the mode, occurring 30% of the time. The probability that no goat is stuck now becomes a tiny 0.218%, which is expected.
What is surprising, however, is how neither the mode, 4, nor the average, 3.93, is even closer to the higher half of the curve. In fact, the probability of having 6 or more goats stuck on the roof, even as goats now prefer the sky, drops sharply, indicates that there's more that meets the eye. Indeed, what the higher floor preference also yields is the freeing up of lower rooms, such that should a goat prefer those, then with a high probability it would be unoccupied. Even if it is occupied, floors right above it likely will be free, therefore not stranding the goat to the roof.