



August 5, 2022
Magritte the bowler is back! This time, he is competing head-to-head against fellow bowler Fosse. However, rather than knocking down 10 pins arranged in a triangular formation, they are trying to knock down \(N^2\) pins (where \(N\) is some very, very large number) arranged in a rhombus, as shown below:

When Magritte rolls, he always knocks down the topmost pin. Then, if any pin gets knocked down, it has a 50 percent chance of knocking down either of the two pins directly behind it, independently of each other. (If there is only one pin directly behind it, then it too has a 50 percent chance of being knocked over.)
Fosse is a stronger bowler than Magritte. Like Magritte, she always knocks down the topmost pin. But each pin that’s knocked down then has a 70 percent chance (rather than Magritte’s 50 percent) of knocking down any of the pins directly behind it.
What are Magritte’s and Fosse’s respective probabilities of knocking down the bottommost pin in the rhombus formation?
From numerical computations, Magritte (0.5)'s probability goes to 0 as \(N \to \infty\), whereas for Fosse (0.7), the probability converges to 81.63%.
Explanation:
Let's consider the general case here. First of all, why \(N^2\) pins? Well, to prove it, let's write \(N^2\) a slightly different way:
\begin{align} &N^2 \\ =& (N - 1 + 1)^2 \\ =& (N - 1)^2 + 2(N - 1) + 1 \\ =& (N - 1)[(N - 1) + 2] + 1 \\ =& (N - 1)(N + 1) + 1 \\ =& (N - 1)N + (N - 1) + 1 \\ =& 2\left(\frac{(N-1)N}{2}\right) + N \\ =& 2(1 + 2 + 3 + \dots + (N - 1)) + N \\ \end{align}
Where the last step is obtained from the famous formula derived by Gauss.
From the above re-writing of \(N^2\), you can see that the \(N\) represents the number of pins in the middle row. There are \((N - 1)\) rows above the middle row that are arranged in a triangular pattern with 1 pin on row 1, 2 pins on row 2, \(k\) pins on row \(k\), and so on, until the \((N - 1)\)th row. Then, the triangular pattern is reflected symmetrically about the middle row to form the rhombus shape of \(N^2\) bowling pins.
Let \(p\) be the probability that a pin knocks down the ones behind it, as described in the problem. A key observation is that in general, there will be two pins that are in front of the current pin as seen below:
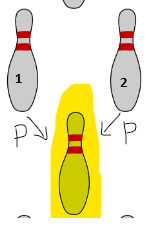
The highlighted pin gets knocked down if at least one of the pins ahead of it knocks it down. This is with probability \(p\) times the probability of the parent pin getting knocked down in the first place. Therefore, letting \(p_1\) and \(p_2\) be the probability that pin 1 and pin 2 that are directly in front of the current pin getting knocked down, respectively, the probability that the current pin gets knocked down is shown in the Venn diagram below.
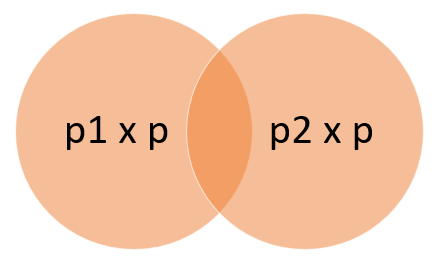
The overlap is when both pin 1 and pin 2 knocks down the current pin, which we must subtract from the total probability of either pin knocking down the current pin. The probability that the current pin gets knocked down is simply the union of the two events shown above, which becomes:
\begin{align} &\text{Prob. of the current pin getting knocked down} \\ =& p_1 \times p + p_2 \times p - (p_1 \times p)(p_2 \times p) \\ \end{align}
Please note that we can even generalize it to the pins on the edge by treating an imaginary "pin 2" with probability of knocking down the edge pin being 0. This will help with the algorithm implementation for the numerical computation, which we are going to explore next.
For this Riddler, I have decided to apply numerical computation to find the answer. The algorithm is simplified by having every pin having two predecessors (edge pins will have one of them having zero probability of knocking down). This yields the following function to get the matrix of probabilities for the entire \(N^2\) pins as a function of \(N\) and \(p\):
function [outProbMatrix, finalProb] = getPinMatrix(N, p)
%getPinMatrix Gets the probability map of the pin matrix given N and p
% Problem from Riddler:
% https://fivethirtyeight.com/features/can-you-knock-down-the-last-bowling-pin/
rows = 2*N - 1;
probMatrix = zeros(rows, N);
probMatrix(1, 1) = 1;
% First, we populate the upper portion
for i = 2:N
for j = 1:N
if j == 1
probMatrix(i, j) = probMatrix(i-1, j) * p;
else
probMatrix(i, j) = p*(probMatrix(i-1, j-1) + probMatrix(i-1, j)) - ...
(p^2)*probMatrix(i-1, j-1)*probMatrix(i-1, j);
end
end
end
% Then, we populate the lower portion
for i = N+1:rows
for j = ((i-N) + 1):N
probMatrix(i, j) = p*(probMatrix(i-1, j-1) + probMatrix(i-1, j)) - ...
(p^2)*probMatrix(i-1, j-1)*probMatrix(i-1, j);
end
end
% Next we clear all zero probabilities from probMatrix
probMatrix(probMatrix == 0) = NaN;
...
% Final prob
finalProb = probMatrix(end, end);
end
The complete numerical computation code is available upon request.
Let's look at some initial results now. For \(N = 10\), i.e. 100 pins, we have the following for Magritte's performance (\(p = 0.5\)).

The bottommost pin here has a 9.6% chance of being knocked over.
Now for Fosse, again with \(N = 10\), i.e. 100 pins, but now \(p = 0.7\), we have:
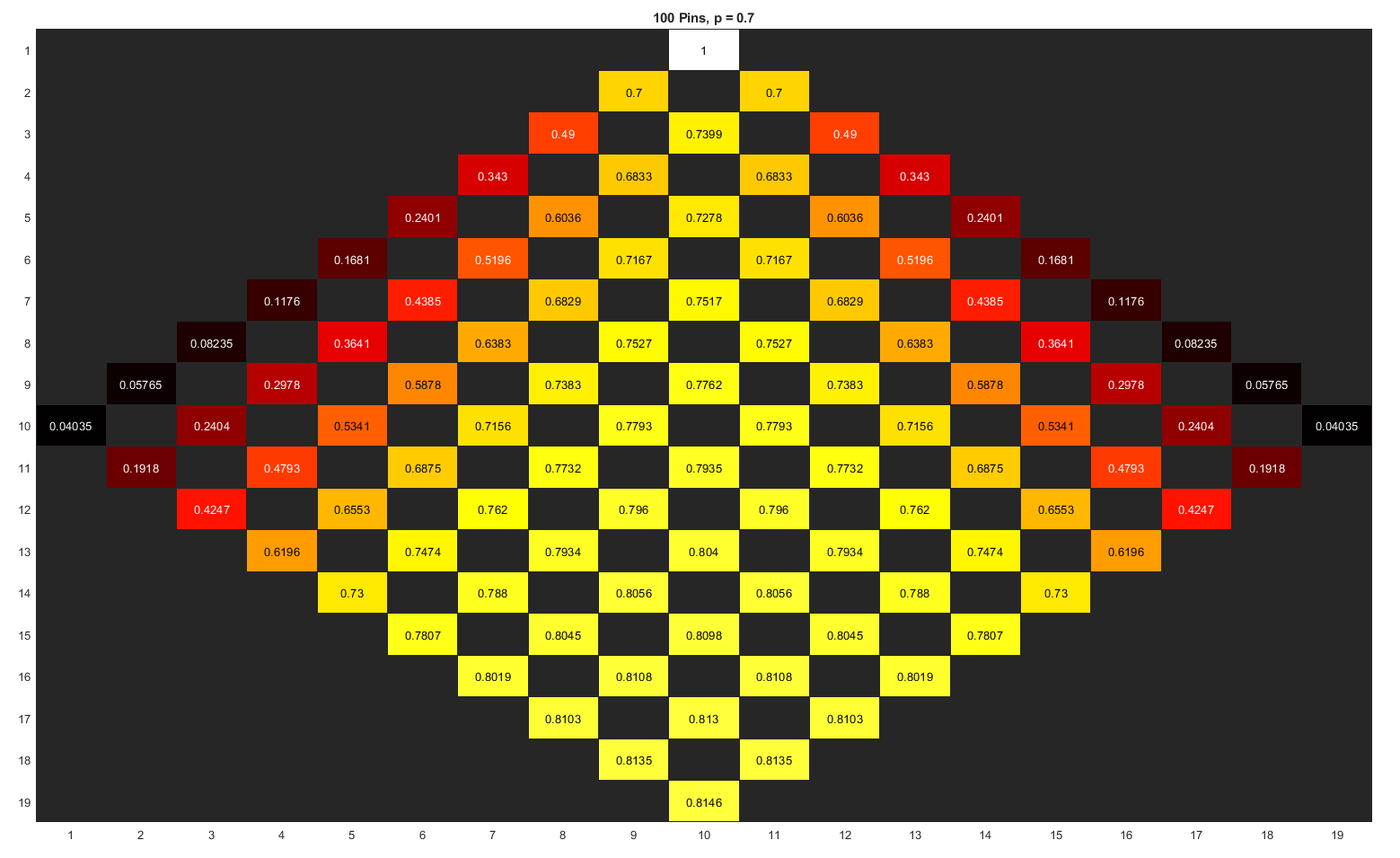
Now the bottommost pin here has an 81.5% chance of being knocked over, despite only a 0.2 increase in probability for each pin from Magritte's case.
An interesting observation here is that the probability of the next row's pins getting knocked over is NOT going to decrease exponentially, because it can be knocked over by up to two pins in front of it. In fact, every pin behind the middle row will have two "parent" pins, and hence if the probability \(p\) is greater than 0.5, we can expect the bottommost pin to be knocked over more likely than not.
Now, to answer the Riddler, we will look at the probability for large values of \(N\), and draw some conclusions for different values of \(p\).
For \(p = 0.5\), it appears that the probability of the bottommost pin knocking over converges to 0 as \(N \to \infty\), roughly linearly with respect to \(N\). However, for \(p = 0.7\), the value seems to converge to a probability as \(N\) becomes larger. That probability is 0.8163.
In fact, I plotted the probability of the bottommost pin topping over as a function of both \(N\) and \(p\), for various values of \(p\) ranging from 0.1 to 0.9 and for \(N\) going from 2 to 1000 (i.e. number of pins going from 4 to 1 million), and observed the following:
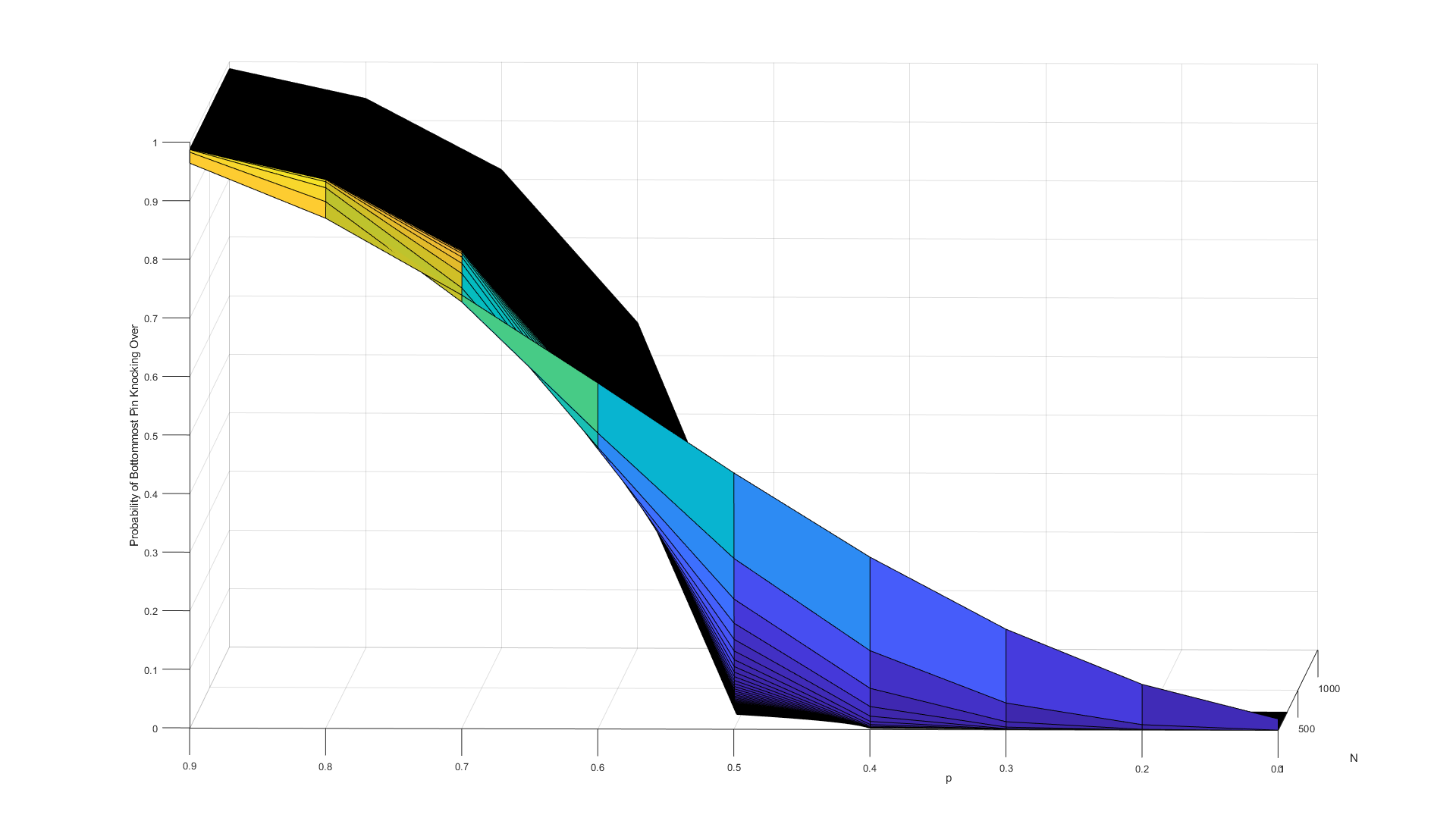

From the above viewpoints of the graph, one can see that as \(p > 0.5\) the probability will converge to a value for \(N \to \infty\). On the other hand, for \(p \leq 0.5\), the probability converges to 0. For a fixed \(N\), the probability increases to 1 in a sigmoidal curve.
I'll leave it to readers to determine an expression of the probability in terms of \(N\) and \(p\).