August 19, 2022
79%.
Explanation:
We are using Monte-Carlo simulation with code written using MATLAB.
function res = fullDosage(N)
% Returns simulated result of whether a full dosage was taken given N days
% to take N*1.5 pills. Assume N*1.5 is a positive integer.
pillRow = N*1.5; % Assume integer
numPills = pillRow;
pills = ones(numPills, 2); % Each column represents half a pill
for k = 1:N-1
% Each day one takes equivalent of three half-pills
pillVec = randperm(numPills);
pillRows = pillVec(1:3); % First three pills ready to be taken
if sum(pills(pillRows(1), :)) == 2
% Full pill
pills(pillRows(1), :) = 0;
if sum(pills(pillRows(2), :)) == 2
% Second is also a full pill
pills(pillRows(2), 1) = 0; % Take half the second pill
else
% Second is a half pill
pills(pillRows(2), :) = 0;
end
else
% Half pill for the first pill
pills(pillRows(1), :) = 0;
if sum(pills(pillRows(2), :)) == 2
% Second is a full pill, take all
pills(pillRows(2), :) = 0;
else
% Second is also a half pill
pills(pillRows(2), 2) = 0;
% We need third pill
if sum(pills(pillRows(3), :)) == 2
% Take half of third pill
pills(pillRows(3), 1) = 0;
else
% Take the remaining half of third pill
pills(pillRows(3), :) = 0;
end
end
end
% Update pill vec to get rid of all pills with zeros
pills = pills(any(pills, 2), :);
[numPills, ~] = size(pills);
end
% On the last day, check whether we have two pills or three (only options)
if numPills == 2
res = 1;
else
res = 0;
end
end
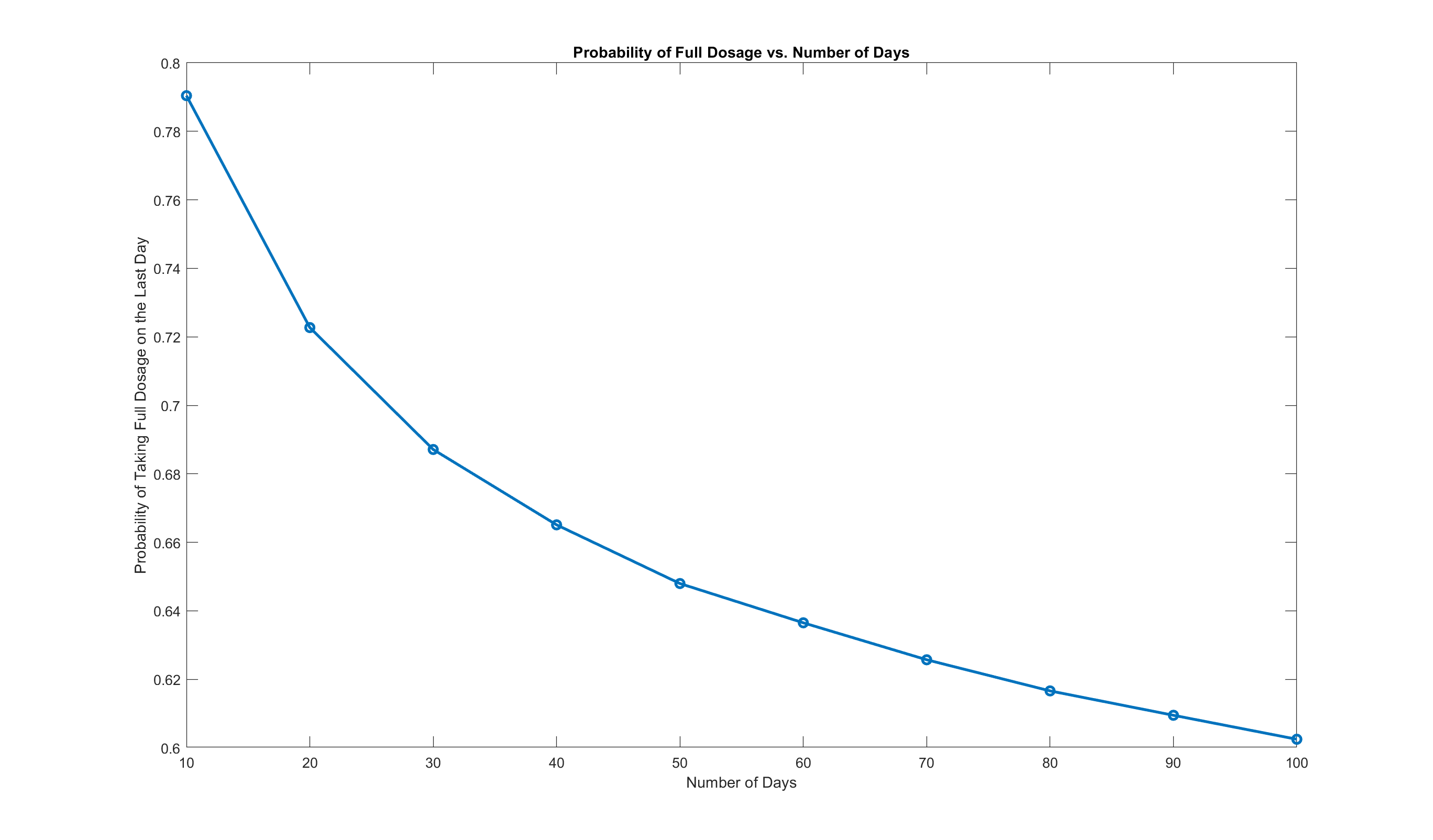
For \(N = 10\) days, the probability is \(79\%\) with 1 million simulations.
Below are the probabilities for N = 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 days obtained via Monte-Carlo with 1 million simulations. Notice that as N increases, the probabilities of finding full dosage goes down roughly in an exponential decay fashion, which is not surprising as the number of half pills in the bottle increases with more days and therefore more chances to cut pills in half.