



October 8, 2021
You are walking along a perfectly straight road one day. One hundred feet in front of you, and then another 100 feet to the left of the road, there is a lamppost (see the diagram below). You can’t be sure, but you briefly spot a doppelgänger on the other side of the lamppost, the same distance away. You look again, but now all you see is the lamppost. Perhaps your eyes were playing tricks on you.

Or perhaps your doppelgänger is now obscured by the lamppost. You start walking along the road, getting closer to the lamppost, but your doppelganger remains hidden. Feeling outmaneuvered, you suspect that your doppelgänger moves precisely twice as fast as you at all times. However, unlike you, they are not constrained to a straight road, and can move more freely in two dimensions.
You walk a total of 200 feet (always forward, never backward), so that the lamppost is now 100 feet back and 100 feet left of the road. Still no sign of the speedy doppelgänger, who is assuredly still obscured by the lamppost.
At this point, you contemplate chasing down the doppelgänger more directly. But before doing so, you wonder: What is the farthest the doppelgänger could be from the lamppost? (Again, assume they move precisely twice as fast as you at all times, that they started symmetrically opposite from you and that they were obscured by the lamppost at all times.)
Maximum distance here is 2.89 units or 289 feet between lamppost and your doppelgänger. This is when \(t = 2\) and you are at \((1, -1)\) while your doppelgänger is at approximately \((-2.04, 2.04)\). Location in units. Convert to feet by multiplying by 100.
Explanation:
When the Editor says this is one of the hardest Riddler Classics ever, he might not be kidding:
I'm not saying #ThisWeeksRiddler Classic will be the hardest ever, but it's up there. (At least, IMHO.)
— Zach Wissner-Gross (@xaqwg) October 6, 2021
I hope y'all don't have weekend plans.
We are going to attempt it anyways, because I love a good challenge!
Let's flip the grid clockwise by 90 degrees so that we don't run into any infinite slope shenanigans. We are going to let 1 unit = 100 feet, such that you are moving at exactly 1 unit per second. Your body-double, therefore, is moving at 2 units per second. Let's map the units onto a Cartesian plane, with the lamppost at the origin (0, 0). Then, you will be at the upper left (-1, 1), and moving due south (so your y-coordinate will go from 1 to -1) at 1 unit/sec. Meanwhile, your doppelgänger will start at the lower right and moving at 2 units/sec, except both his/her x and y-coordinates can change, provided the mysterious figure is blocked in view by the lamppost at all times.
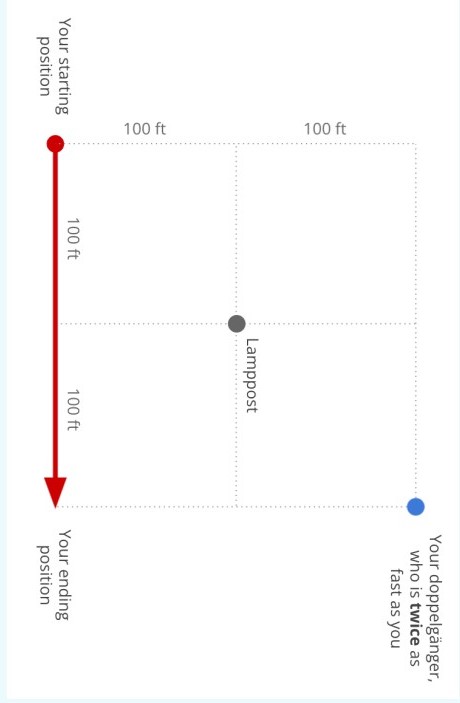
Finally, let \(t\) represent time. Let \(y_0\) represent your y-coordinate position, and let \(x, y\) be the coordinates of your doppelgänger. Please note that \(0 \leq t \leq 2\) as we are assuming 1 unit = 100 ft and you are moving at 1 unit / sec.
To solve any complex problem, it helps to understand it. There are no better way than trying a few simple cases. The key here is that the pesky constraint of your doppelgänger being obscured by the lamppost from your point of view needs to be active at all times. What if we relax it? We will obtain good upper bounds on the solution and reveal key insights to solve the actual problem.
Please note that the lower bound is \(2\sqrt{2} \approx 2.83\) units, obtained at the starting position.
For a very loose upper bound, let us only have the doppelgänger be obscured by the lamppost at \(t = 2\), i.e. the ending position. We can determine that position exactly, using the following thought process.
At \(t = 2\), you will be at (-1, -1) while the lamppost, hopefully being inanimate, is still at (0, 0). That means the line of sight follows the equation \(y = x\). Therefore, the doppelgänger's final position must be \((x, x)\), as \(y = x\). Finally, the speed constraint must be satisfied at all times. After 2 seconds, you moved 2 units, and so your clone counterpart would've moved \(2 \times 2 = 4\) units, albeit in two dimensions.
Using the Euclidean distance formula, we get:
\begin{align} \sqrt{(x - 1)^2 + (x + 1)^2} &= 4 \\ (x - 1)^2 + (x + 1)^2 &= 16 \\ 2x^2 + 2 &= 16 \\ x^2 + 1 &= 8 \\ x^2 &= 7 \\ x &= \pm \sqrt{7} \\ \end{align}
Ignoring the negative solution as the doppelgänger must be on the other side of the lamppost, we get his/her final position to be \((\sqrt{7}, \sqrt{7})\).
This means the maximum distance between you and your doppelgänger when the view is obscured is: \(\sqrt{2}(\sqrt{7} + 1) \approx 5.16\) units.
However, the final answer isn't the above, unfortunately, because the line-of-sight (LOS) constraint must be satisfied at ALL times, and not just at the end. We can improve upon our answer, i.e. obtaining a tighter upper-bound, by enforcing another of LOS constraint, say at halfway \(t = 1\). Again, we note the distance the doppelgänger could have travelled at this point and any LOS constraints. Here at \(t = 1\), your y-coordinate is 0, and so the LOS is parallel to the x-axis. Therefore, the doppelgänger's y-coordinate must be 0 as well. Furthermore, the doppelgänger would've moved by 2 units after 1 second. This yields:
\begin{align} \sqrt{(x - 1)^2 + (0 + 1)^2} &= 2 \\ (x - 1)^2 + 1 &= 4 \\ (x - 1)^2 &= 3 \\ x &= \pm \sqrt{3} + 1 \\ \end{align}
Again we ignore the negative solution. So at \(t = 1\), the doppelgänger is at \((\sqrt{3} + 1, 0)\) and is \(\sqrt{3} + 2 \approx 3.73\) units away from you.
Keep going to \(t = 2\), we use the doppelgänger's position at \(t = 1\) to do another incremental update, this time noting that his/her coordinates must be the same as now LOS is the line \(y = x\).
\begin{align} \sqrt{(x - (\sqrt{3} + 1))^2 + (x - 0)^2} &= 2 \\ (x - (\sqrt{3} + 1))^2 + x^2 &= 4 \\ x &= 1 \text{ or } \sqrt{3} \\ \end{align}
If \(x = 1\) then the doppelgänger is back at the original position at the other side in a symmetric fashion. If \(x = \sqrt{3}\) the doppelgänger is at a farther location as compared to you at \((\sqrt{3}, \sqrt{3})\). This yields the maximum distance, and a tighter upper bound, to be \(\sqrt{2}(\sqrt{3} + 1) \approx 3.86\) units.
So to recap, we obtained our absolute lower bound to be approximately 2.83 units and our upper bound to be 5.16 units. The final answer is between those bounds and we have a candidate answer of 3.86 units with only two levels of quantization!
The exercise in the previous section yielded an algorithm to solve for the actual answer: finer quantizations. If we divide your path down the y-coordinate to be \(N = 2/\Delta t\) levels, with each level acting as a "checkpoint" enforcing the doppelgänger to satisfy the LOS constraint, we can, in a similar fashion as above, incrementally obtain the final position of the body-double. Then, among the steps, we identify the coordinate pairings between you and your doppelgänger that yields the largest distance, and that will be the correct answer. To put everything mathematically, we must have the following constraints:
For \(N\) levels, \(\Delta t = 2/N\) and at level \(k\), the update equation is:
\begin{align} (x_k - x_{k-1})^2 + ((k\Delta t - 1)x_k - y_{k-1})^2 &= (2\Delta t)^2 \\ \end{align}
Applying the algorithm for \(N = 100\) levels, we obtain an interesting path taken by the doppelgänger:
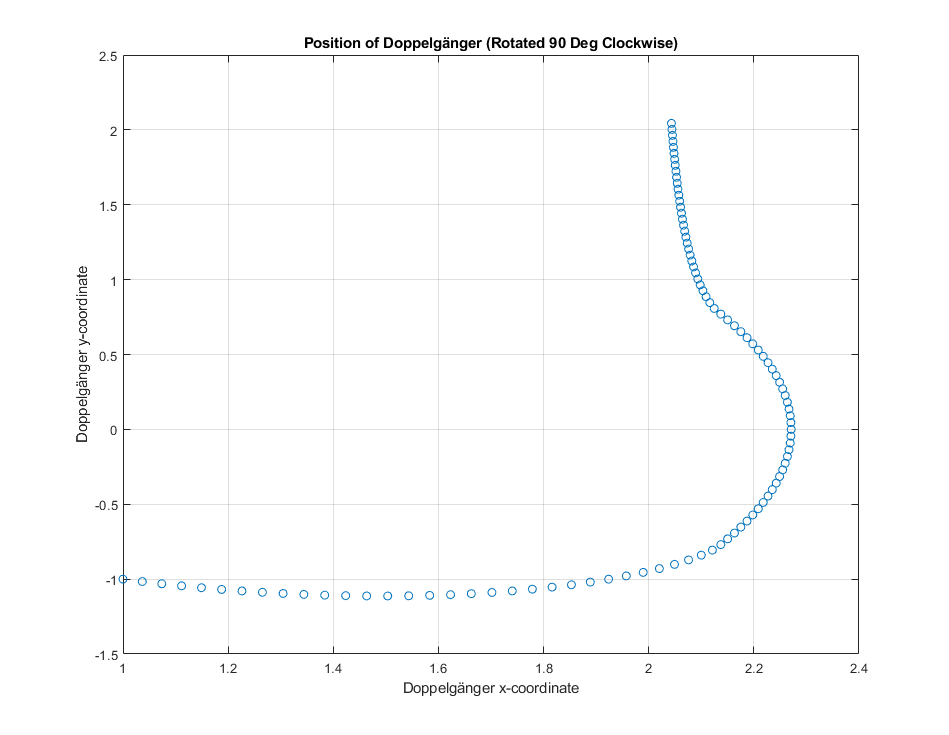
The distance between you and your doppelgänger varies because you are moving too, but the maximum distance seems to be obtained at the final position:
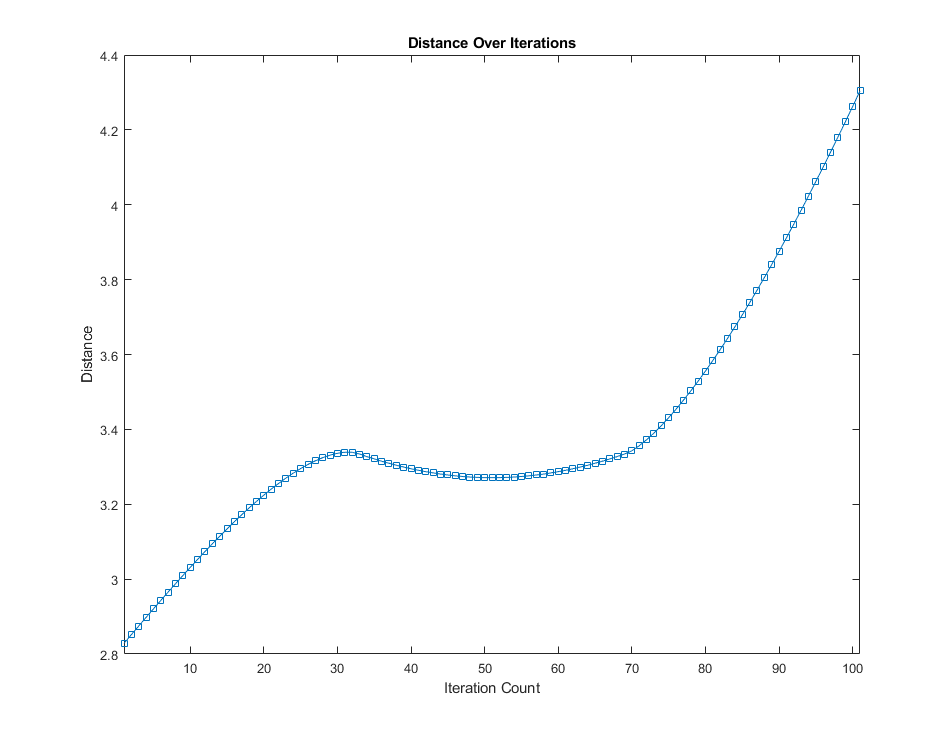
This algorithm yields a final result of:
Maximum distance is 4.30 units or 430 feet. This is when \(t = 2\) and you are at \((-1, -1)\) while your doppelgänger is at approximately \((2.04, 2.04)\). Location in units. Convert to feet by multiplying by 100. Rotating back to original positioning, this means when you are at \((1, -1)\) while your doppelgänger is at approximately \((-2.04, 2.04)\).
We can use the above algorithm to calculate the distances between the doppelgänger and the lamppost instead of the distance between you and the doppelgänger by keeping track of the lamppost's coordinate instead of yours, which is always (0, 0).
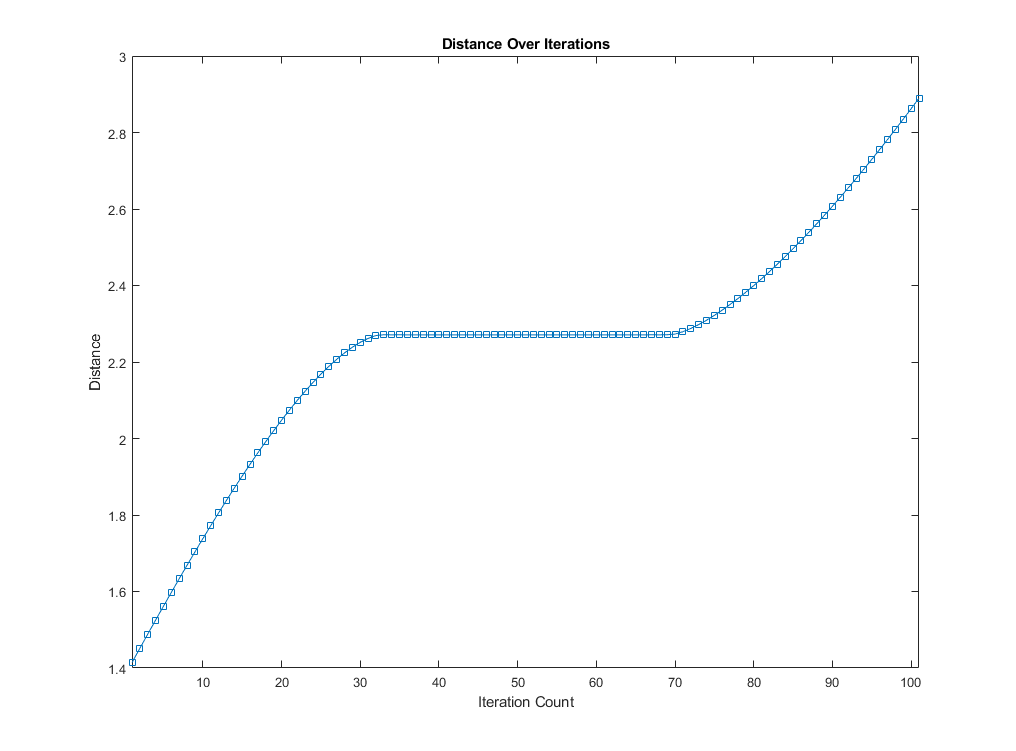
Maximum distance here is 2.89 units or 289 feet between lamppost and your doppelgänger. This is when \(t = 2\) and you are at \((-1, -1)\) while your doppelgänger is at approximately \((2.04, 2.04)\). Location in units. Convert to feet by multiplying by 100. Rotating back to original positioning, this means when you are at \((1, -1)\) while your doppelgänger is at approximately \((-2.04, 2.04)\).