



November 26, 2021
Trig the turkey cannot fly. And so, instead of flying, he decides to jump as far as he can with a running start up one of the famed Sinusoidal Hills, all of which are precisely the same size.
Trig knows that he cannot jump a horizontal distance of more than two hills. Also, he prefers a smooth takeoff and landing. That is, when he takes off from the ground and lands on it again, the slope of his parabolic trajectory through the air must perfectly match the instantaneous slope of the ground beneath him.
What is the greatest horizontal distance Trig can jump, such that his takeoff and landing are smooth? Again, keep in mind that Trig cannot possibly jump a horizontal distance greater than two hills.
Greatest achievable horizontal distance: 1.4313 hills.
Explanation:
Turkeys are flightless birds, but in spirit of Thanksgiving, where this year one avian dreamer named Trig is grateful for calculus, airtime is possible over the Sinusoidal Hills. An example of such a jump is illustrated as below with a horizontal distance of 1.2 hills:

Here, a "hill" is defined as the horizontal distance between two consecutive peaks of a sinusoidal wave. For example, if the hill's outline is defined by the function \(y = \sin(x)\), then one unit of the "hill" would be of distance \(2\pi\).
The first step in maximizing Trig's horizontal jump distance would be to determine the regions of the hills where he can take off and land. The regions are confined by the constraints described in the problem in words. Therefore, let us represent those constraints in the language of math.
The original set of constraints are given as below:
"Trig knows that he cannot jump a horizontal distance of more than two hills. Also, he prefers a smooth takeoff and landing. That is, when he takes off from the ground and lands on it again, the slope of his parabolic trajectory through the air must perfectly match the instantaneous slope of the ground beneath him."
First, let us define the sinusoidal hills graphically for our problem setup. Without Loss of Generality (WLOG), let the hill take on the function \(y = \cos(x - \pi) + 1\) such that one hill is of the distance \(2\pi\). Doing so translates the original sinusoidal curve to a convenient position where the origin is the ground level for the first hill and the lowest points on the hill are at \(y = 0\). The final shape of the hills look like below, sketched out for three hills:
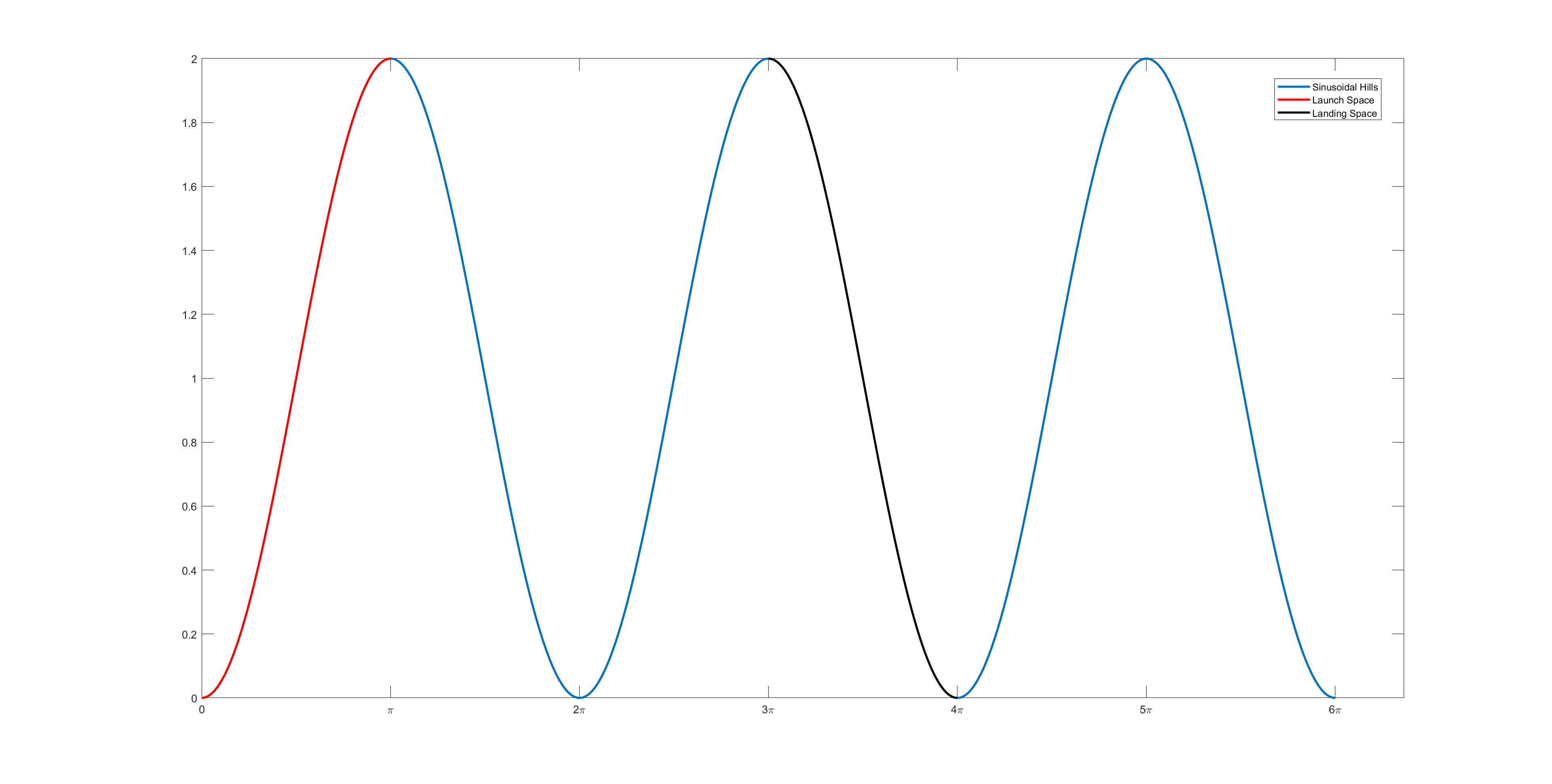
The red and the black regions of hill's surface mark the possible launch and landing spaces for Trig, respectively. This is derived from the following constraints:
WLOG, let Trig take off somewhere along hill 1. Then, it is clear that he cannot get past hill 3. However, with constraints 2 and 3 together, it is clear that at most he can land on the backside of hill 2. Due to gravity, the parabola is concave, and so for the rising part of the trajectory, the slope must be positive. Since by constraint 3 it must match that of the hill at the takeoff point, Trig can only launch himself on the frontside of hill 1, as past the peak the slope becomes negative, and he would dive headfirst into the ground (ouch!).
Similarly, near the landing spot, the concave parabola has a negative slope and so he must land on the backside of a hill. If he attempted to land on the frontside of a hill, where the slope is positive, he would again crash into it. Furthermore, if he launched himself on the frontside of hill 1, he cannot reach backside of hill 3 as that would be more than two hills apart. Therefore, the farthest of a hill he can possibly arrive after his flight would be the backside of hill 2.
Now there is a subtler fourth constraint, which is dictated by physics (and common sense), which reads:
Clearly, as Trig is not made of antimatter-ish substances, he cannot pass through ground while in flight. The moment the parabolic trajectory crosses with the hill's surface, his flight is over.
This further constraints the launch and landing spaces for Trig, using a second derivative analysis. Let's take a look:
\begin{align} y &= \cos(x - \pi) + 1 \\ y' &= -\sin(x - \pi) \\ y'' &= -\cos(x - \pi) \\ \end{align}
Why do we care about the hill's second derivative? Well, due to constraint 4, if the launch point on the hill is convex at the point of launch, then the flight would be over immediately as the parabola would be below the hill's surface, causing Trig to dive straight into the ground! Similarly, if the landing point is convex for the hill, then there is no way for Trig to land smoothly unless he somehow tunnels beneath the hill, which is not allowed. As the hill is not entirely convex nor concave, we need to find the inflection points to determine the divide between the convex and concave regions of the hill's surface, such that we ensure the launch and landing spaces both fall in the latter region. This is done via the hill's second derivative, \(y'' = -\cos(x - \pi)\).
Setting \(y'' = 0\), we get an inflection point for \(x \in [0, \, \pi]\) at \(x = \frac{\pi}{2}\). Similarly, for \(x \in [3\pi, \, 4\pi]\) on the second hill, we have the inflection point at \(x = \frac{7\pi}{2}\). Trig can only launch and land at the regions of hill where the surface is concave, i.e. when \(y'' < 0\). This further reduces the available spaces as illustrated below.
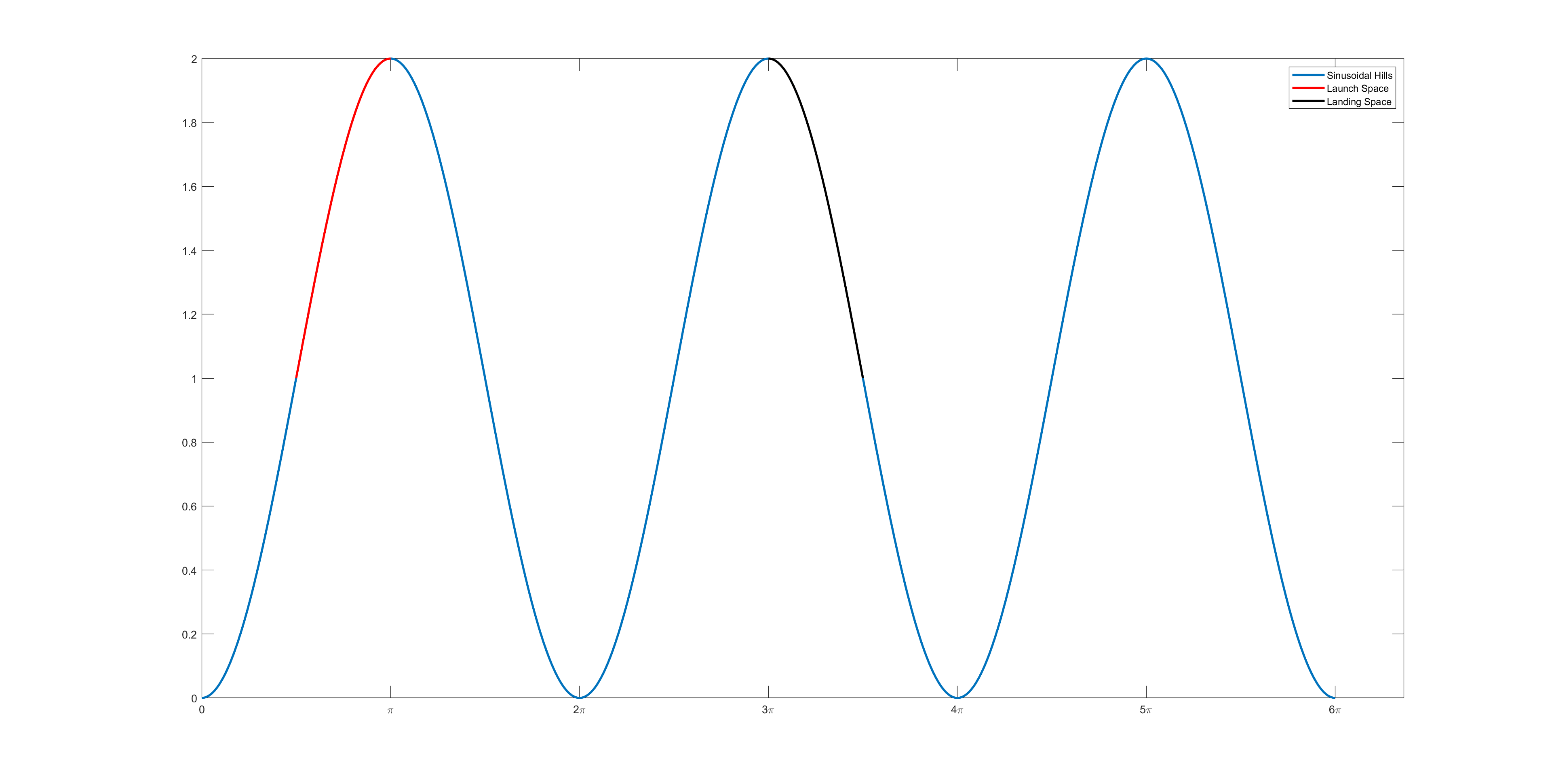
Now that we've established our search spaces, we will make use of an important property of the flight's trajectory--symmetry. As the saying goes, what goes up, must come down. Should Trig decide to take off at a point within the launch space as depicted in the graph above, there must be the corresponding slope for landing, within the described landing space. That is, if Trig takes off with slope \(s\), then the landing slope must be \(-s\). The parabola is also symmetric about the vertical line passing through its vertex. This means, should Trig maximizes his horizontal jump distance, the leap will cross hill 1 to hill 2, and the vertex will have x-coordinate \(2\pi\).
This greatly simplifies the equation for the parabolic flight trajectory, as instead of using the standard form for a quadratic function, we can resort to the vertex form. Let the coordinates of the vertex be \((2\pi, h)\), then Trig's flight trajectory is:
\begin{align} y &= -a(x - 2\pi)^2 + h \\ \end{align}
For some \(a > 0\). I explicitly wrote down the negative sign to highlight that the parabola must be concave, due to gravity.
Remark: the parameter \(a\) is what we are implicitly optimizing here, as it determines the "fatness" of the parabolic curve and hence where Trig should take off (and land). Of course, in the ensuing sections of the explanation, we do not need to optimize for \(a\) by itself, as it will soon be clear.
By symmetry, we only need to write down the constraints on the launch side of the trajectory, as the landing side necessarily follows similar slopes. Given \(x \in [\frac{\pi}{2}, \, \pi]\) (the launch space), we need to have the launching parabola point touching the hill, this means:
\begin{align} -a(x - 2\pi)^2 + h &= \cos(x - \pi) + 1 \\ \end{align}
We also need the slope of the parabola at the launch point to be equal to that for the hill's surface, for a smooth take off (and landing). This yields:
\begin{align} -2a(x - 2\pi) &= -\sin(x - \pi)\\ \end{align}
Here, we have two unknowns in \(a\) and \(h\), and given \(x\), we have a linear system of equations for those two unknowns.
\begin{align} \begin{bmatrix} -(x - 2\pi)^2 & 1 \\ -2(x - 2\pi) & 0 \end{bmatrix} \begin{bmatrix} a \\ h \end{bmatrix}&= \begin{bmatrix} \cos(x - \pi) + 1 \\ -\sin(x - \pi) \end{bmatrix}\\ \end{align}
Solving for \(a\) and \(h\) gives a possible parabolic flight trajectory for Trig, at launch point \(x\). This can be done in MATLAB as follows:
function [y, a, h] = jump(x, x0)
% x0 is the starting point in the launch space
A = [-(x0-2*pi)^2, 1
-2*(x0-2*pi), 0];
b = [cos(x0-pi) + 1
-sin(x0-pi)];
sol = A\b;
a = sol(1);
h = sol(2);
% The jump equation
y = -a.*(x - 2*pi).^2 + h;
end
We need to ensure that the flight is feasible. This translates to checking every point for \(x \in [x_0, \, x_0 + 2(2\pi - x_0)]\) such that the parabola is greater than or equal to the hill's surface, that is, constraint 4. At any stage the parabola dives below the hill, the flight would end. This is done in MATLAB as below:
function [res, y, a, h, x] = isJumpFeasible(dist)
% Given the distance in units of hills, determine if the jump is
% feasible or not.
hillLength = 2*pi;
hillHalfLength = (dist/2)*hillLength;
xStart = 2*pi - (hillHalfLength);
xEnd = 2*pi + (hillHalfLength);
x = linspace(xStart, xEnd, 1000);
% Calculate feasibility
[y, a, h] = jump(x, xStart);
yHill = hill(x);
% Give a slight tolerance for precision error
tol = 1e-12;
flightError = flightError + tol;
flightError = y - yHill;
res = all(flightError >= 0);
end
Finally, in order to ensure Trig has the best time of his life enjoying as much airtime as possible, we are going to maximize his horizontal distance using the above function to search within the designated search space until a feasible jump is found. From our reduction of search space we already know that we need to search between 1 and 1.5 hills. From the problem's given, we know that 1.2 hills is possible. Therefore, the following binary search starting with \([1.2, \, 1.5]\) hills, with stopping condition of 1e-10, is employed in MATLAB:
function [y, a, h, x, dist] = searchFeasibleJumps()
% Use binary search to find feasible jumps
distStart = 1.2;
distEnd = 1.5;
dist = (distStart + distEnd)/2;
distDiff = distEnd - distStart;
tol = 1e-10;
[feasible, y, a, h, x] = isJumpFeasible(dist);
while distDiff > tol
fprintf('Distance searched = %.5f\n', dist);
if feasible
distStart = dist;
else
distEnd = dist;
end
dist = (distStart + distEnd)/2;
[feasible, y, a, h, x] = isJumpFeasible(dist);
distDiff = distEnd - distStart;
end
end
A small tolerance is required as the difference can be quite minute, especially near the end points. It quickly converges:
>> [y, a, h, x, dist] = searchFeasibleJumps(); Distance searched = 1.35000 Distance searched = 1.42500 Distance searched = 1.46250 Distance searched = 1.44375 Distance searched = 1.43438 Distance searched = 1.42969 Distance searched = 1.43203 Distance searched = 1.43086 Distance searched = 1.43145 Distance searched = 1.43115 Distance searched = 1.43130 Distance searched = 1.43123 Distance searched = 1.43126 Distance searched = 1.43124 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125 Distance searched = 1.43125
Let's check the result:
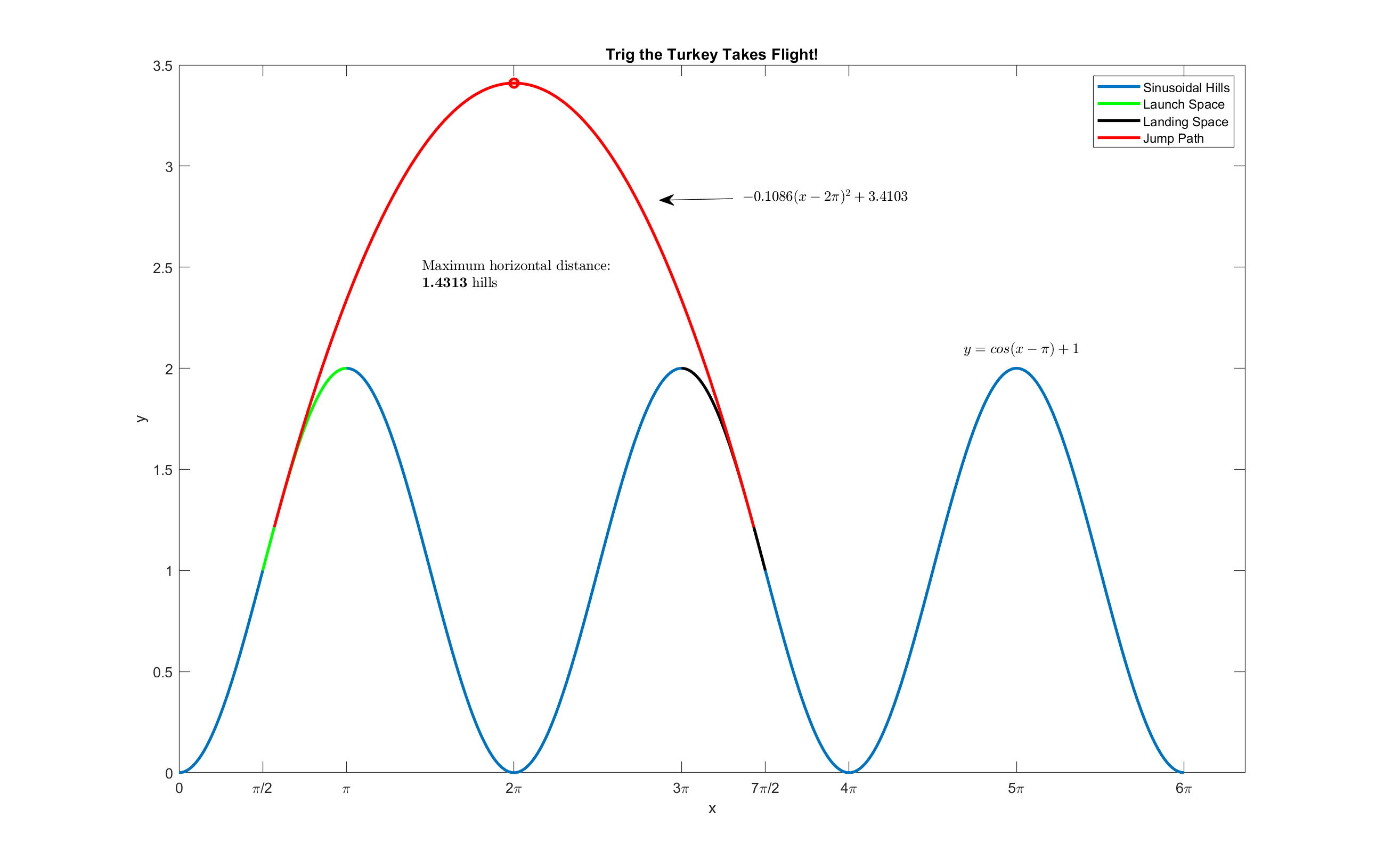
We have the final flight trajectory as:
\begin{align} y &= -0.1086(x - 2\pi)^2 + 3.4103\\ \end{align}
Trig would launch himself at \(x = 1.7868 = 0.5687\pi\) and land at \(x = 10.7796 = 3.4313\pi\). This covers a total horizontal distance of 1.4313 hills. He would also achieve a maximum height of 3.4103, equivalent to more than half a hill!
For completeness, below is the difference between the flight trajectory and the hill's surface for the maximum horizontal distance flight, showing that the parabolic curve is always greater than or equal to the hill's surface:

The difference graph is very reminiscent of a bell curve.
Happy flight!