



January 7, 2022
From Leonard Cohen comes a timely matter of touchdowns:
In the Riddler Football League, you are coaching the Arizona Ordinals against your opponent, the Detroit Lines, and your team is down by 14 points. You can assume that you have exactly two remaining possessions (i.e., opportunities to score), and that Detroit will score no more points.
For those unfamiliar with American football, a touchdown is worth 6 points. After each touchdown, you can decide whether to go for 1 extra point or 2 extra points. You happen to have a great kicker on your team, and your chances of scoring 1 extra point (should you go for it) are 100 percent. Meanwhile, scoring 2 extra points is no sure thing — suppose that your team’s probability of success is some value p.
If the teams are tied at the end of regulation, the game proceeds to overtime, which you have a 50 percent chance of winning. (Assuming ties are not allowed.)
What is the minimum value of p such that you’d go for 2 extra points after your team’s first touchdown (i.e., when you’re down 8 points)?
Minimum \(p\) required is \(\boxed{\frac{3-\sqrt{5}}{2}}\) or approximately 0.382
Explanation:
First, we re-phrase the question in a mathematical manner so that we can obtain the correct value of \(p\). Please note that there are two scenarios:
Only in the second scenario does the Ordinals' chance of winning the game involve \(p\). Therefore, the first scenario can be thought of as the baseline. Since the 1PAT is guaranteed to be converted, and Ordinals are trailing the Lines by exactly 14 points, then the probability of going into overtime (OT) is 100% and hence the probability that the Ordinals will win the game, as given in the puzzle, would be 50% for the first case.
Therefore, we have the baseline at 0.5. We need a value of \(p\) such that in the second scenario where 2PAT is involved, the probability of winning the game for the Ordinals exceed 0.5. We also assume that each conversion is independent of the other.
Now that we have worded the puzzle mathematically, we can calculate the probability of winning the game for the Ordinals in the second scenario in terms of \(p\), so that we can then create an inequality against the baseline to determine the minimum value of \(p\). Here, we have three scenarios. I will describe them like this: 0-a-b = (a + b), where 0 is the number of points gained for the Ordinals at the start of the comeback, after trailing by 14. The values of \(a\) and \(b\) are the points gained by the Ordinals after the first and second touchdowns, including the PATs, respectively. The total points gained in the end is simply the sum of a and b.
The above depictions are helpful because on each of the dashes (-) there is a probability associated with it. We also can see the end result to determine whether the game is won, tied, or lost at the end of regulation.
The scenarios are determined by logic, with the goal of maximizing Ordinals' winning, or let the head coach walk the plank. Therefore, there is no such things like "0-8-8 = 16" because if the 2PAT is converted after the first touchdown, then there is no reason not to go for the surefire 1PAT after the second touchdown, as 15 is good enough for the win. On the other hand, if the 2PAT is no good after the first touchdown, we must go for the 2PAT after the second TD otherwise the Ordinals lose outright. This is why there is also no scenarios such as "0-6-7 = 13".
Now let's calculate each individual scenario's probability of occurrence.
The first scenario wins outright; the second goes into OT, and the third loses outright. Therefore, the overall probability of winning for the Ordinals involving 2PAT is:
\begin{align} &P(\text{winning}) \\ &= p + \frac{(1-p)p}{2} \\ \end{align}
We have the inequality:
\begin{align} p + \frac{(1-p)p}{2} &> 0.5 \\ 2p + p(1-p) &> 1 \\ 2p + p - p^2 &> 1 \\ 3p - 1 &> p^2 \\ p^2 &< 3p - 1 \\ p^2 - 3p + 1 &< 0 \\ \end{align}
Solving the inequality, and keeping in mind that \(0 \leq p \leq 1\) as \(p\) represents a probability, we get:
\begin{align} \frac{3-\sqrt{5}}{2} < p < 1 \\ \end{align}
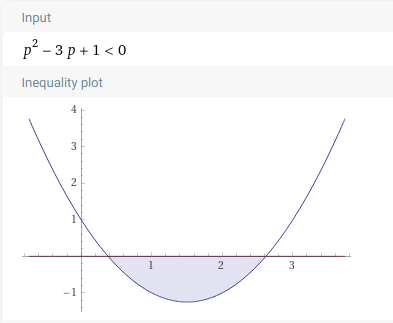
Hence, the minimum \(p\) required is \(\boxed{\frac{3-\sqrt{5}}{2}}\) or approximately 0.382.
The Arizona Ordinals then successfully defeated the Cleveland Brownian Motion to win the inaugural Riddler Football League's Super Bowl.