Riddler Express: January 8, 2021

David Ding

January 9, 2021

Cutting Squares

From Rob Peacock comes a matter of squaring a multitude of squares:

There are many ways to slice a big square into smaller squares (not necessarily of equal size), so that the smaller squares don’t overlap, while still making up the entire area of the big square.

For example, you can slice the big square into four smaller squares, each a quarter of the area of the big square. Or you could slice it into seven squares, if you take one of those four squares and slice it into four yet smaller squares.

What whole numbers of squares can you not slice the big square into?

Answer: Only whole numbers you cannot slice into are 2, 3, and 5.

Explanation:

Try as you might, you cannot cut a square into 2, 3, or 5 pieces. (Please try it out!). You can cut a square into any arbitrary even number of pieces greater than 2 using the following scheme:

squares

This will cut the big square into \(2(n+1)\) pieces, for \(n = 1, 2, 3, \dots\) by scaling the top left square accordingly. Therefore, for the smallest value of \(n\) we have four squares, which is simply dividing the big square into four quadrants.

We can additionally cut the big square into \(k + 3\) pieces, for \(k = 4, 6, 8, 10, 12, \dots\) by the following step:

  1. Pick \(n = 1, 2, 3, \dots\) and divide the big square into \(2(n+1)\) pieces from the configuration illustrated earlier.
  2. Select one of the sub-squares and divide that into four quadrants. This will add three more squares divided.

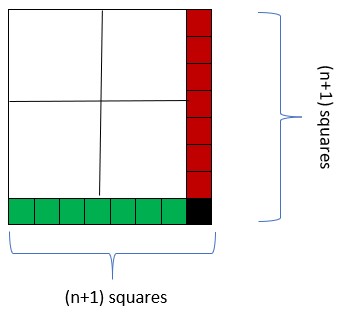
squares2

The procedure above subsequently allows one to divide a big square into any odd number of pieces greater than 5.