January 17, 2021
From Lucas Jaeger comes a “flute-iful” challenge:
You’re a contestant on the hit new game show, “You Bet Your Fife.” On the show, a random real number (i.e., decimals are allowed) is chosen between 0 and 100. Your job is to guess a value that is less than this randomly chosen number. Your reward for winning is a novelty fife that is valued precisely at your guess. For example, if the number is 75 and you guess 5, you’d win a $5 fife, but if you’d guessed 60, you’d win a $60 fife. Meanwhile, a guess of 80 would win you nothing.
What number should you guess to maximize the average value of your fifing winnings?
Answer: You should guess $50, for an expected average winning of $25.
Explanation:
Let \(X\) be the random variable denoting the value of the fife. From the problem, let us assume that \(X\) is uniformly distributed between 0 and 100 for now. Therefore, the cumulative distribution function (CDF) of \(X\) is as follows:
\begin{align} P(X \leq x) &= F_X(x) \\ &= \begin{cases} 0, & \quad x < 0 \\ \frac{x}{100}, & \quad 0 \leq x \leq 100 \\ 1, & \quad x > 100 \end{cases} \\ \end{align}
Furthermore, let \(g\) denote the value of your guess (for \(0 \leq g \leq 100\)). Based on the problem setup, your winnings are determined as follows:
\begin{equation} \text{Your winnings} = \begin{cases} g, & \quad g < X \\ 0, & \quad g \geq X \\ \end{cases} \end{equation}
Putting everything together, your expected winnings come to an expression as follows:
\begin{align} \text{Your expected winnings} &= gP(g < X) \\ &= gP(X > g) \\ &= g(1 - P(X \leq g)) \\ &= g(1 - F_X(g)) \\ &= g\left(1 - \frac{g}{100}\right) \\ &= \frac{-g^2}{100} + g \end{align}
It follows that we need to find the maximium of our expressions, which is just finding the vertex of the inverted parabola. Converting to vertex form:
\begin{align} \frac{-g^2}{100} + g &= -\frac{1}{100}(g^2 - 100g) \\ &= -\frac{1}{100}(g^2 - 100g + 50^2 - 50^2) \\ &= -\frac{1}{100}[(g - 50)^2 - 2500)] \\ &= -\frac{1}{100}(g - 50)^2 + 25 \\ \end{align}
Therefore the maximum value of \(g\) is 50, and the maximum expected winnings is $25, obtained on average when you guess $50.
Although the guess of $50 appears somewhat expected, it was purely due to the consequence of the distribution of the values for the fife, which in the previous case was uniform. In general, the optimal guess \(g\), which yields an expected winnings of \(g(1 - F_X(g))\), need not to be $50, for it depends on how \(X\) is distributed.
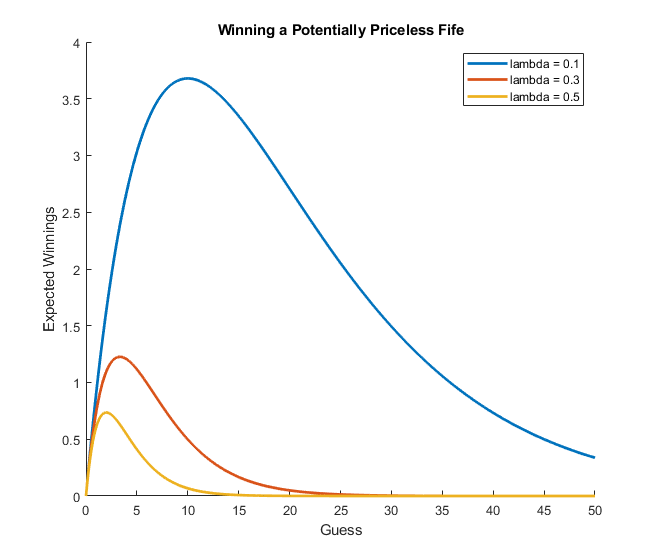
For example, say \(X\) is distributed with an exponential distribution with parameter \(\lambda > 0\). With this distribution, \(X\) goes from 0 to infinity, with larger the \(\lambda\) value, the more likely \(X\) will be concentrated towards the low end of things. With this distribution, the price of fife can go up to infinity (i.e. you have a chance to win a price-less fife!), but it is more likely for the fife to be worth very little. Assume the same game rules apply, what should be your strategy of guessing? Well, we apply the same optimization on our expression:
\begin{align} \text{Your expected winnings} &= g(1 - P(X \leq g)) \\ &= g(1 - F_X(g)) \\ &= g[(1 - (1 - e^{-\lambda g})] \\ f(g) &= ge^{-\lambda g} \\ 0 = f'(g) &= e^{-\lambda g} - g \lambda e^{-\lambda g} \\ 0 &= e^{-\lambda g} (1 - g \lambda) \\ g \lambda &= 1 \\ g^* &= \frac{1}{\lambda} \end{align}
That is, your optimal guess should be the inverse of the \(\lambda\). As \(\lambda\) increases, it is more likely that the fife will be worth less, and so you should also lower your guess accordingly. With the optimal guess \(g^*\), your maximized expected winnings become:
\begin{align} \text{Your maximized expected winnings} &= g^*e^{-\lambda g^*} \\ &= \frac{e^{-\frac{\lambda}{\lambda}}}{\lambda} \\ &= \boxed{\frac{e}{\lambda}} \end{align}
It makes sense, as when \(\lambda\) is closer to 0, the value of the fife is spread out more between 0 and infinity, and by guessing \(\frac{1}{\lambda}\) you have a chance of winning a very valuable fife. On the other hand, as \(\lambda \to \infty\), more and more values of fife will be concentrated on the low-end, and therefore you are forced to have your optimal guess also approach 0, and thereby also squeezing your expected maximum winnings to 0.
The graphs below show the hypothetical distributions of the fife values if it can go all the way to infinity. Of course, the more valuable a fife can be, the rarer it becomes. I only considered cases where \(\lambda\) values are less than one, so that we can maximize our expected fife value to be greater than a dollar.
