David Ding: Riddler Express February 5, 2021

By all accounts, Riddler Nation had a lot of fun hunting for the mysterious numbers a few weeks back. So here’s what we’re going to do: For the next four weeks, the Riddler Express will feature a similar puzzle that combines multiplication and logic. We’ll be calling these CrossProducts.

For your first weekly CrossProduct, there are five three-digit numbers — each belongs in a row of the table below, with one digit per cell. The products of the three digits of each number are shown in the rightmost column. Meanwhile, the products of the digits in the hundreds, tens and ones places, respectively, are shown in the bottom row.

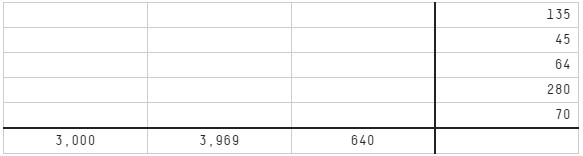
Can you find all five three-digit numbers and complete the table?

Prime factor the numbers on the right-hand column, and collect factors keeping only the possible combinations that are between 1 and 9, inclusive. After that, I used an exhaustive search algorithm balancing time spent shrinking the search set and the algorithm's actual search time. That is, I do the work on the rows, and MATLAB handles the rest with the columns. I did this by only considering the digits that are possible for each row and let the machine take care of the columns. Algorithm written in MATLAB:

   
%% Author: David Ding
% February 6, 2021
clear;
close all;
clc;

%% Start of solver
% For each row, we populate the only possible values
posValSet = {
    [3, 5, 9];
    [1, 3, 5, 9];
    [1, 2, 4, 8];
    [5, 7, 8];
    [2, 5, 7];
};

horizVals = [135; 45; 64; 280; 70];
vertVals = [3000, 3969, 640];

% Exhaustive Search
finalAns = zeros(5, 3);

% Populate a guess using the allowed values only
searchValSet = cell(5, 1);
for k = 1:5
    searchValSet{k} = popListOfPossibleAnswers(posValSet{k}, horizVals(k));
end

%% Search
for a = 1:length(searchValSet{1})
    finalAns(1, :) = deal(searchValSet{1}(a, :));
    for b = 1:length(searchValSet{2})
        finalAns(2, :) = deal(searchValSet{2}(b, :));
        for c = 1:length(searchValSet{3})
            finalAns(3, :) = deal(searchValSet{3}(c, :));
            for d = 1:length(searchValSet{4})
                finalAns(4, :) = deal(searchValSet{4}(d, :));
                for e = 1:length(searchValSet{5})
                    finalAns(5, :) = deal(searchValSet{5}(e, :));
                    fprintf('%d %d %d %d %d\n',...
                                    a, b, c, d, e);
                    % Verify answer
                    if checkAnswer(finalAns, vertVals)
                        % We've found it!
                        disp('Got it!');
                        return;
                    end
                end
            end
        end
    end
end

finalAns

%% Populate answers row
function vecList = popListOfPossibleAnswers(posVals, desiredVal)
    len = length(posVals);
    vecList = NaN(len^3, 3);
    k = 1;
    for a = 1:len
        for b = 1:len
            for c = 1:len
                
                % Horizontal check
                prod = posVals(a) * posVals(b) * posVals(c);
                if prod ~= desiredVal
                    continue;
                end
                vecList(k, 1) = posVals(a);
                vecList(k, 2) = posVals(b);
                vecList(k, 3) = posVals(c);
                k = k + 1;
            end
        end
    end
    
    vecList = rmmissing(vecList);
end

%% Check answer helper function
function res = checkAnswer(finalAns, vertVals)
    res = true;
    
    % Vertical
    for j = 1:3
        prodVec = cumprod(finalAns(:, j));
        prod = prodVec(end);
        if prod ~= vertVals(j)
           res = false;
           return;
        end
    end
end


>> finalAns

finalAns =

     3     9     5
     5     9     1
     8     1     8
     5     7     8
     5     7     2

For the sake of completeness, allow me to share the thinking process for one of the rows in constructing the "posValSet". The only possible values for the first row are 3, 5, and 9. Why is that? The reason is because after coarsely factoring the product for that row, 135, into 3 times 5 times 9, I simply re-arrange in my head the other possible factors and see if I can still end up with three that are between 1 and 9, inclusive. Of course, in doing so I must not forget the "1" as a possible factor. Now, "9" is not prime, so it can be decomposed into two "3"'s. But at least one of the "3"'s must be then absorbed into one of the other factors, since we are only allowed three factors at all times. Where can it go? If you absorb one of the decomposed "3"'s from the "9" into the first "3", we get back the factor of "9". Putting the "3" into the "5", we get "15", which is outside the single-digits range. Similarly, there is no way to have "1" as one of the single-digit factors and have the other two factors both be single digits at the same time. Hence, 3, 5, and 9 are the only possible values. After this analysis, the MATLAB algorithm takes it from here for the rest of the search.

Riddler Express: February 5, 2021

Mystery Sudoku Mini