



March 19, 2021

The two larger squares are congruent, and the smaller square makes a 45 degree angle with one of the larger squares. Both larger squares touch the circle at one corner, while the smaller square touches the circle at two corners.
How many times greater is the area of one of the larger squares than the area of the smaller square?
Answer: \(\frac{9}{2}\) times larger.
Explanation:
Before diving into the puzzle, I must remark on the aesthetically pleasing design of the felt-tip drawing neatly outlining the circle and the squares. The whole picture gives off a cartoonish vibe but of course, the geometry involved here is anything but child's play. Nonetheless, it is a very interesting puzzle and the key to solve requires knowing a concept of the invariant. The invariant is a quantity in a math puzzle that remains constant, for which multiple ways of acquiring that constant would yield useful equations that would in turn derive the final answer. Since this puzzle involves a circle, the invariant we can consider here is the radius of the circle, which of course, by definition, must be constant.
The gist of the solution is in the diagram below, in which I will further explain in detail. Note, it would be helpful to have the following diagram along side with you so you don't have to scroll back and forth.
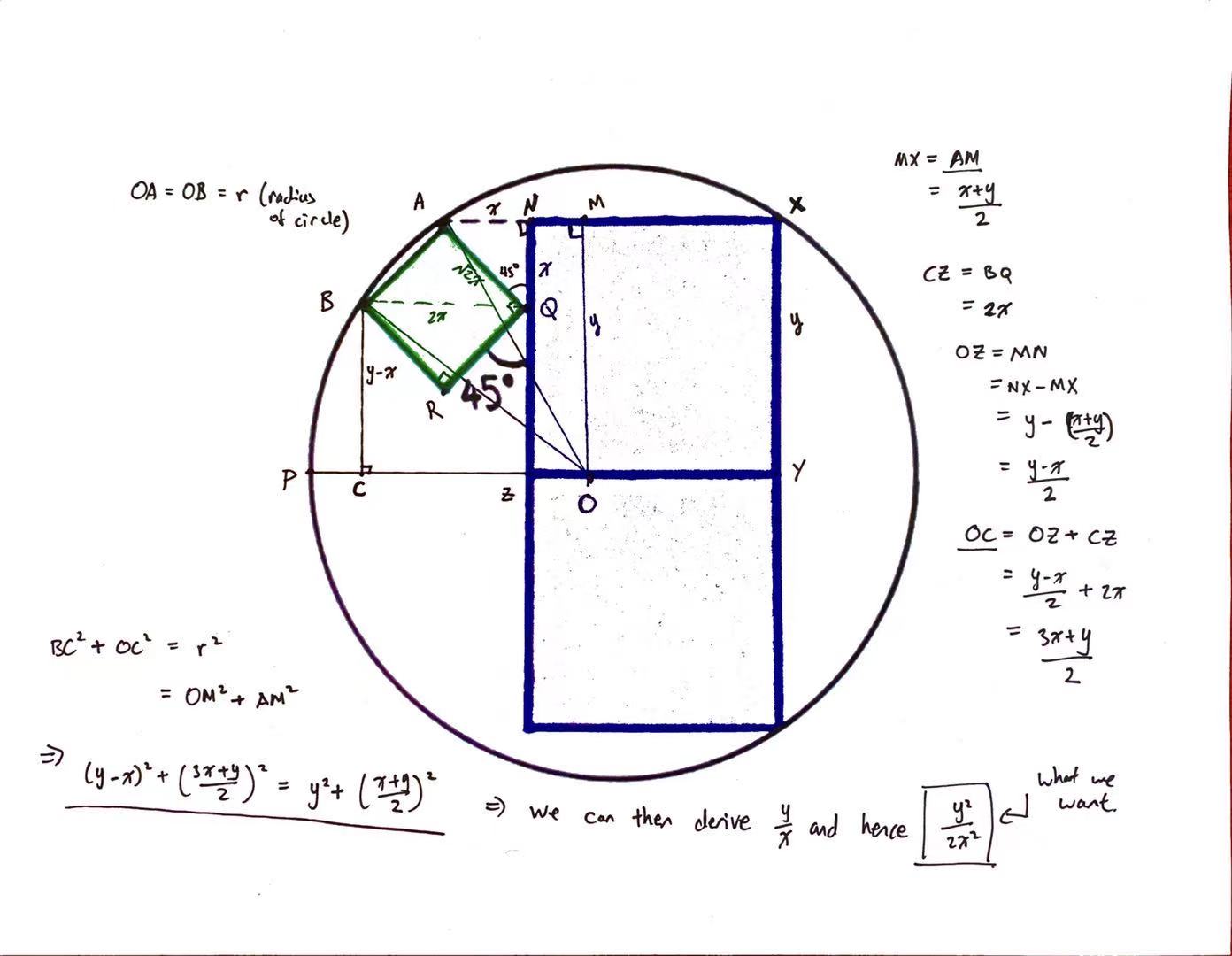
We let the larger square \(NXYZ\) have side length of \(y\), and the smaller square \(ABRQ\) have side length of \(\sqrt{2} x \), as seen in the above diagram. Thus, the answer of the ratio of the larger square's area to that of the smaller square would be \(\frac{y^2}{2x^2}\). Since the two larger squares are congruent, and each has the one corner opposite of the other touching the circle on the same side, then by symmetry, line segment \(YZ\) must lie on the diameter of the circle. Therefore, we let point \(O\) on \(YZ\) to be the center of the circle, and extend \(YZ\) to the circle meeting at point \(P\). We also extend line segment \(NX\) to the circle meeting at point \(A\).
The invariant here, which is the radius of the circle, comes into play for two line segments, \(OA\) and \(OB\), for which both have length \(r\) for being the two of the radii of the circle.
We drop a line segment parallel to \(XY\) from \(O\) to \(NX\) meeting at point \(M\). Since \(NXYZ\) is a square, therefore \(OM\) is perpendicular to \(NX\) and also has length of \(y\). This makes triangle \(AMO\) a right-angled triangle. Since angle \(RQZ\) is given to be 45 degrees and angle \(RQA\) is 90 degrees because \(ABRQ\) is also a square, that makes angle \(AQN\) 45 degrees. Therefore, triangle \(ANQ\) is a 45-45-90 special triangle, which means the side lengths shares a \(1:1:\sqrt{2}\) ratio. We assigned \(AQ\) to have length of \(\sqrt{2} x \), therefore making both \(AN\) and \(NQ\) to have lengths of \(x\).
Next, by symmetry, since both points \(A\) and \(X\) are touching the circle, that means \(AX\) is a chord of the circle. Then, since \(OM\) is perpendicular to \(AX\) and \(O\) is the center, that makes \(M\) the midpoint of \(AX\). How long is \(AX\)? It is exactly \(x + y\). Therefore, \(AM\) has length \(\frac{x+y}{2}\).
Applying Pythagorean Theorem on triangle \(AMO\), we have:
\begin{align} AM^2 + MO^2 &= OA^2 \\ \left(\frac{x+y}{2}\right)^2 + y^2 &= r^2 \\ \end{align}
Remember the above equation!
We drop a line segment parallel to \(NZ\) from point \(B\) onto \(OP\) meeting at point \(C\). Again since \(NXYZ\) is a square, therefore \(BC\) is perpendicular to \(OP\) and it makes triangle \(BCO\) a right-angled triangle as well. Since angle \(RQZ\) is given to be 45 degrees, it can be deduced that \(BQ\) is parallel to \(CO\). This makes \(BC\) having length of \(y - x\).
The last clue we need to gather is the length of \(CO\). We can write \(CO = CZ + ZO\). For \(CZ\), we observe it has the same length as \(BQ\), and then we can apply Pythagorean Theorem on triangle \(ABQ\) to derive the value of \(BQ\) to be \(2x\) and hence also for \(CZ\). For \(ZO\) we can write it as:
\begin{align} ZO &= ZY - OY \\ &= NX - MX \\ &= NX - AM \\ &= y - \frac{x+y}{2} \\ &= \frac{y-x}{2} \end{align}
Therefore, we derive \(CO\) as:
\begin{align} CO &= CZ - ZO \\ &= 2x + \frac{y-x}{2} \\ &= \frac{3x + y}{2} \end{align}
Now applying Pythagorean Theorem on triangle \(BCO\), we have:
\begin{align} BC^2 + CO^2 &= OB^2 \\ (y-x)^2 + \left(\frac{3x+y}{2}\right)^2 &= r^2 \\ \end{align}
Also remember the above equation!
We now have two different ways of finding out the value of the invariant \(r\). We can reap the reward now by equation the two expressions for it and obtain our final answer.
\begin{align} (y-x)^2 + \left(\frac{3x+y}{2}\right)^2 &= \left(\frac{x+y}{2}\right)^2 + y^2 \\ 4(y-x)^2 + (3x+y)^2 &= (x+y)^2 + 4y^2 \\ 4y^2 - 8xy + 4x^2 + 9x^2 + 6xy + y^2 &= x^2 + 2xy + y^2 + 4y^2 \\ 5y^2 - 2xy + 13x^2 &= x^2 + 2xy + 5y^2 \\ 12x^2 - 4xy &= 0 \\ 3x^2 &= xy \end{align}
Now, \(x\) is a length measure and cannot be 0, and hence we can cancel one \(x\) from both sides of the above equation. We finally get:
\begin{align} 3x^2 &= xy \\ 3x &= y \\ \frac{y}{x} &= 3 \\ \end{align}
The quantity we are looking for is \(\frac{y^2}{2x^2}\), and so we apply the finishing touches:
\begin{align} \frac{y^2}{2x^2} &= \frac{1}{2} \left(\frac{y}{x}\right)^2 \\ &= \frac{1}{2} (3)^2 \\ &= \boxed{\frac{9}{2}} \end{align}
The invariant has turned our variables into a concrete answer indeed!